Система с 2-мя плоскостями симметрии

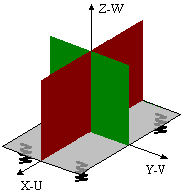
Плоскости симметрии: XOZ, YOZ. 4 амортизатора под основанием блока.

Исходная система из 6-ти уравнений разбивается на 2 независимых уравнения и 2 системы по 2 уравнения. Из 2-х независимых уравнений точно определяются две дискретные частоты, а 2-е системы решаются упрощенно методом Релея.

т.к. для оси Z условия не изменились.

Для упрощенного определения парциальных частот, входящих в неравенство Релея, составляются связки координат. Для данной системы в связку входят 2 координаты и составляются 2 подобные связки.

В связки объединяются именно те координаты, которые входят в системы из двух дифференциальных уравнений.

Связки составляются следующим образом: выделяются координатные оси, лежащие в плоскости симметрии, но не на пересечении этих плоскостей. Координата, характеризующая поворотное движение вокруг одной оси, объединяется с координатой, характеризующей поступательное движение вдоль другой оси.

В нашем случае объединяются координаты [X-V], [Y-U]............. Для каждой связки записывается неравенство Релея:

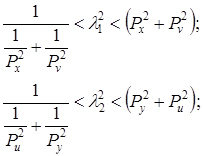
Физически, наличие подобных связок координат проявляется в единстве движений, объединенных связкой, например: придавая блоку поступательное движение вдоль оси V (для 1-ой связки), мы тем самым заставляем двигаться блок вдоль оси «Х». Для 2-ой связки: раскачивая блок вокруг «Y», мы тем самым заставляем его двигаться вдоль оси U. Если связок нет, то движение вдоль Z или вокруг Z существует без каких-либо побочных движений, т.е. независимо.

В записи «Т» и «П», представленными в квадратичной форме, присутствовали члены:

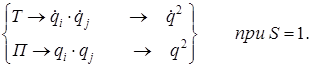
Для одной степени свободы степени вырождались в квадраты, но для S >1, например для S = 2 имеем:

эта взаимосвязь – математическая трактовка физического явления связанности движений.

Для S = 3

т.е. присутствуют все парные произведения, следовательно, все движения связаны между собой.

Дата добавления: 2015-07-11