Система 3-мя плоскостями симметрии.

Симметрия: XOY XOZ YOZ

1. равенство (симметричность) масс выдерживается автоматически, т.к. оси проходят через центр тяжести блока и через них проводится плоскость симметрии.

2. Координаты амортизаторов должны быть симметричны.

1. система с 8-ю амортизаторами: 4 под и 4 над блоком. Ее свойства:

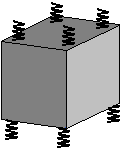
а) случай не рациональный, т.к. велико число амортизаторов, вполне достаточно 4-х. б) усложнен расчет и монтаж такой системы.

2. Система с 4-мя амортизаторами Z_i = 0. т.е. установка амортизаторов в плоскости XOY. Свойства: при строгом решении исходной системы 6-ти дифференциальных уравнений подобной системы амортизации наличие плоскости симметрии масс частей блоков, координат установки амортизаторов, жесткостные параметры

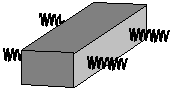
амортизации приводит к тому, что указанная система уравнений разбивается на 6 независимых уравнений (см. раздел вынужденных колебаний). Из каждого уравнения может быть точно определена своя собственная частота.

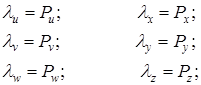
это вырожденное неравенство Релея-Донкерли для N = 1.

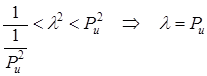
Т.о. на оси частот имеем 6 дискретных собственных частот.

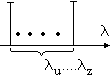
Во всех случаях желательно сужать диапазон собственных частот. В данной системе амортизации возможно при введении дополнительных условий добиться равенства всех собственных частот: 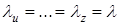и на оси частот имеем одну дискретную частоту.

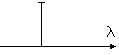
Эти дополнительные условия имеют вид:

а) динамические жесткости амортизаторов и соответствующие системы амортизации по всем направлениям должны быть равны: C_gu = C_gv = C_gw

б) координаты «Х» амортизаторов должны быть равны радиусу инерции относительно оси «Y», а координаты «Y» амортизаторов должны быть равны радиусу инерции относительно оси «Х».

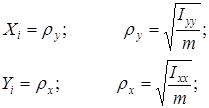
Недостаток: для большинства амортизаторов: C_gu = C_gv 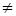C_gw.

Дата добавления: 2015-07-11