Динамический расчет системы амортизации.

2.1 Определение жесткостных и инерционных параметров системы.

2.2. Определение парциальных частот системы.

2.3 Определение собственных частот системы.

2.4 Определение коэффициента динамичности.

2.5 Определение ускорения объекта.

Статический расчет системы

1. Определение координат центра тяжести объекта.

Исходным при проектировании системы амортизации являются не только параметры внешних механических воздействий, но и законченная компоновка устройства, т.е. считаются известными габариты устройства (блока), место установки, габариты, масса различных частей блока (узлы, детали), кроме этого существуют ограничения на типоразмер амортизатора. Необходимым является наличие всех характеристик для применяемого типа амортизатора.

На первом этапе в блоке аппаратуры выделяются элементарные узлы простейшей геометрической формы. При этом из сборочного чертежа всегда можно определить координаты центра тяжести этого элементарного блока относительно любой выбранной первоначальной системы координат. Для элементарного блока координаты его центра тяжести должны быть достаточно просто определяемыми. Рекомендуется первоначально выбирать систему так, чтобы одна ось проходила через ребро куба.

Масса элементарного блока также должна быть известна. Форма элементарного блока должна быть такова, чтобы определение собственных моментов инерции этого блока было возможно по таблицам (см. п. 2.1).

X, Y, Z – координаты центра тяжести блока, относительно выбранной первоначально системы координат.

- сила тяжести блока.

После определения центра тяжести блока координатные оси переносятся в эту точку и весь последующий расчет ведется относительно этих новых координат.

2. Определение реакций амортизаторов.

Различают две схемы нагружения амортизаторов: а) однонаправленная схема; б) пространственная схема нагружения.

а) Однонаправленная схема нагружения должна отвечать следующим условиям:

- реакция амортизаторов и нагрузка на них образуют систему паралельных сил;

- блок в положении равновесия должен устанавливаться без перекосов;

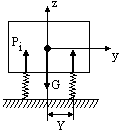
G - суммарный вес блока

P_i -реакции амортизаторов

Эта система возможна при установке блоков без перекосов.

В однонаправленной схеме нагружения неизвестной является реакция амортизатора и число неизвестных зависит от количества амортизаторов. Реакции амортизаторов определяются на основе уравнений статистики. Для однонаправленной схемы:

My = 0; Mx = 0; n – число амортизаторов;

при n = 3, ищем P₁, P₂, P₃, (система из 3-х уравнений). При n = 3 система статически определима, и мы из исходной системы непосредственно находим три неизвестных реакции. При n = 4 система статически неопределима и необходимо четвертое уравнение. Его получают за счет введения дополнительного условия на расположение амортизаторов.

Дополнительные условия задаются за счет соответствующего выбора координат установки амортизаторов. Для такой системы P₁ = P₂ = P₃ = P₄ = G/4. Здесь дополнительное условие – симметрия амортизаторов – вылилось в подобное решение системы.

1.

Всегда при и реакция P₁ = P₂ = … = P_n = G/n

2. Здесь дополнительное условие таково:

P1+P2 = P3+P4; (P1+P4)b’ = (P2+P3)b; P2 = P3; P1 = P4.

для того, чтобы система была статически определима необходимо задать n = 3 дополнительных условий.

б) Пространственная схема нагружения.

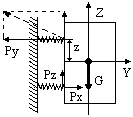
- не однонаправленная схема (произвольное нагружение). Здесь кроме вертикальных нагрузок возникают составляющие по другим направлениям. Реакция – векторная сумма реакций по трем составляющим: Pi = {Pzi; Pxi; Pyi}

т.о. для пространственной схемы нагружения неизвестными являются не реакции, а составляющие реакций. При n амортизаторах имеем 3n неизвестных.

Из 6-ти уравнений определяем 6 неизвестных. Т.о. число дополнительных условий, которое необходимо задать 3n –6. Дополнительные условия получаем аналогично как и для схемы а).

Итак, считаем, что нам известны либо реакции (для схемы а), либо составляющие реакций (схема б). На этом расчет закончен.

Дата добавления: 2015-07-11