Теоретические основы решения

Задача 6. Расчёт плоской рамы

Условие задачи

Для плоской стальной рамы известна нагрузка и вид сечения. Рама нагружена распределённой нагрузкой, сосредото­ченной силой и моментом.

требуется: Подобрать размеры поперечного сечения и определить горизонтальное, вертикальное и угловое перемещения сечения .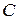

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РЕШЕНИЯ

Рамой называют конструкцию, которая состоит из жёстко соединённых стержней (рис. 6.1, а). Чаще соединение выполняют под прямым углом, a размеры сечения всех стержней одинаковы. Нужно заметить, что стержни мо­гут быть прямолинейными и криволинейными. Здесь рассмотрим расчёт пло­ской рамы с прямолинейными стержнями. Для расчёта составляют расчётную схему плоской рамы, − это геометрический контур реальной рамной конструк­ции, на котором каждый стержень изображается в виде прямого бруса, и по­казана последовательность соединения стержней и нагрузка.

Каждый стержень может быть нагружен распределённой нагрузкой, со­средоточенными силами и моментами. Если эта нагрузка лежит в плоскости рамы, то имеем плоскую раму. В своей плоскости такая рама должна иметь опоры (это опирание или соединение с другими конструкциями). На расчётной схеме изображают заделку, если опора препятствует как линейным, так и угловым перемещениям. Когда реальная опора препятствует только одному перемещению, то на схеме ставят шарнирно-подвижную опору. В случае опоры, препятствующей двум линейным перемещениям в плоскости рамы, на расчётной схеме изображают шарнирно-неподвижную опору. В опорах возникают опорные реакции: в заделке − это вертикальная и горизонтальная силы и изгибающий момент; в шарнирно-подвижной − одна сила; в шарнирно-неподвижной – две взаимно перпендикулярные силы. Причём число опорных реакций не должно быть менее трёх, иначе рама станет геометрически изменяемой, т. е. получит смещения и не будет уравновешен­ной системой. Так рама, изображённая на рис. 6.1, а, имеет шарнирно-непод­вижную и шарнирно-неподвижную опоры, общее количество опорных реак­ций равно трём, и рама геометрически неизменяемая.

Значения опорных реакций необходимы для решения задачи. Опорные реакции и внешние воздействия располагаются в плоскости рамы и создают плоскую систему сил, поэтому для вычисления опорных реакций составляем три уравнения равновесия, чаще используются следующие:

∑ пр z = 0; ∑ мом А = 0, ∑ мом В = 0, (6.1)

оставляя неиспользованное уравнение ∑ пр y = 0 для проверки реакций.

Как известно, для расчётов на прочность и жёсткость необходимо знать внутренние усилия, которые определяются известным методом сечений по правилу РОЗУ: Р азрезать, О тбросить, З аменить, У равновесить. Необходимо выполнить разрез в текущем сечении рамы, рассмотреть отсечённые части и составить уравнения равновесия отсечённой части по уравнениям равновесия в виде:

∑ пр z = 0; ∑ пр y = 0, ∑ мом О = 0, (6.2)

Как видно по рис. 6.1, б, г равновесие отсечённой части рамы соблюдается, если в сечении балки возникают продольная сила N, поперечная сила Q и изгибающий момент M строго определённого значения и направления. Таким обра­зом, в поперечных сечениях плоской рамы возникают три вида внутренних усилий: продольная сила, поперечная сила и изгибающий момент. Поэтому для плоских рам строят три эпюры: эпюры N, Q, M, − это весьма трудоёмкий пункт расчёта рам. Чтобы успешно выполнить построение эпюрнужно пом­нить принципы построения эпюр продольных сил N при растяжении-сжатии и эпюр поперечных сил Q и изгибающих моментов M при плоском изгибе балок.

Так как в сечениях плоских рам возникают одновременно продольные силы 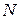, поперечные силы Q и изгибающие моменты M=M_x, то наблюдается сложное сопротивление: совокупность осевого растяжения-сжатия и плоского изгиба. Тогда нормальные напряжения σ определяются суммой напряжений от осевого растяжения-сжатия и плоского изгиба, и касательные напряжения τ, возникают от поперечной силы, эти напряжения вычисляют по формулам:

, .

Но слагаемое часто составляет малую часть от всего нормального напряжения σ; рассуждая с этой точки зрения, иногда говорят, что стержни плоской рамы работают в основном на изгиб. При выполнении проектного расчёта плоских рам, чтобы не усложнять подбор размеров сечения, размеры определяют из условия прочности по нормальным напряжениям изгиба, который имеет вид:

. (6.3)

Условие (6.3) составляют для опасного сечения рамы, которое нужно установить по эпюре изгибающих моментов .

После подбора сечения выполняют проверку прочности с учётом слож­ного сопротивления. Эту проверку начинают с вычисления записанных выше нормальных σ и касательных напряжений τ, потом выявляют опасное сечение и опасную точку этого сечения, вид напряжённого состояния в опасной точке, выбирают и проверяют необходимое условие прочности для сложного сопротивления. Возможные следующие условия прочности.

1. В случае совместного изгиба и продольной силы в опасном сечении условие прочности имеет вид:

. (6.4)

Здесь нужно помнить, что условие (6.4) используется при отсутствии каса­тельных напряжений или их малом значении.

2. При совместном наличии в опасной точке сечения нормальных и касательных напряжений, соизмеримых по величине, условие прочности записываем по теориям прочности, например, по III теории прочности:

. (6.5)

Ниже рассмотрены расчёты для 3-й варианта рамы.

Дата добавления: 2015-07-11