Состязания сигналов и способы их устранения

Из рассмотренного аппарата алгебры логики видно, что он не является временным, то есть параметр «время» отсутствует. Мы предполагали, что логические элементы идеальные, безинерционные. Реальные элементы обладают задержкой распространения сигнала, что приводит к тому, что во время переходных процессов (во время переключения) законы алгебры логики не выполняются и возникают так называемые состязания (гонки) сигналов. Это явление возникает в параллельных цепях логических устройств из-за различия времени распространения сигналов.

Состязания делят на опасные и неопасные. Состязания считаются опасными, если они приводят к возникновению непредусмотренного изменения выходного сигнала.

Различают статические и динамические состязания.

Статические появляются в случае, когда для двух последовательных во времени комбинаций входных сигналов выходной сигнал ЛУ должен оставаться неизменным, а динамические состязания - когда выходной сигнал должен измениться.

Пример статического состязания:

.

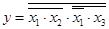Х1	Х2	Х3	f1	f2	y

Рис.43. Схема с состязаниями сигналов и ее карта Карно.

Рассмотрим временные диаграммы при изменении Х1 1 0 с учетом задержки срабатывания элементов.

t1 - t2 - задержка НЕ; t1 - t3 - задержка И - НЕ f1; t2 - t5 - задержка И - НЕ f2; t3 - t4 - задержка И - НЕ у 1 – 0; t5 - t6 - задержка И - НЕ у 0 – 1;  

Рис.44. Временные диаграммы.

В результате при изменении входной переменной Х1 из 1 в 0 на выходе возникает сигнал низкого уровня длительностью t6 - t4, а по завершении переходных процессов на выходе снова устанавливается уровень 1.

Это объясняется тем, что сигнал Х1 в одном случае проходит через 2 элемента (D2, D4), в другом - через 3 (D1, D3, D4). Во втором случае сумма задержек больше. Если подобрать элементы так, чтобы сигнал проходил через элементы D1, D3 быстрее, чем через D2, то выходной сигнал останется постоянно 1. Но практически это невозможно.

Такое состязание, когда оно происходит при единичном выходном сигнале, называется 1- состязание.

Аналогично рассмотренному можно привести пример 0-состязания: при Х1 из 1 в 0.

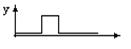
Рис.45. График изменения выходного сигнала при 0-состязании.

В качестве примера динамического состязания можно привести функцию:

при Х1 из 1 в 0.

Рис.46. Схема с динамическими состязаниями.

По степени опасности более неблагоприятны статические состязания, так как появляющийся при наличии состязания импульсный сигнал может быть зафиксирован, запомнен последующими элементами. Динамические состязания иногда даже полезны, так как ведут к повышению быстродействия ЛУ. Следовательно, надо принять меры к недопущению статических состязаний. Выявление состязаний по временной диаграмме представляет трудоемкий процесс и требует опыта. Однако разработаны и формальные методы определения наличия состязаний сигналов в схеме.

Из рассмотренных примеров следует, что причиной возникновения состязаний является невыполнение в схемах в некоторые моменты времени соотношений алгебры логики:

и др.

В результате в эти моменты имеется возможность появления одинаковых значений переменной и ее инверсии. Следовательно, надо выявить, не содержит ли логическое уравнение в СДНФ или СКНФ одновременно переменную и ее инверсию.

Задачу можно решить аналитически и графически с помощью карт Карно. Второй метод - проще.

Статические состязания в схеме существуют тогда и только тогда, когда для любой пары соседних комбинаций входных сигналов с одинаковыми выходными сигналами нет ни одной комбинации, которая бы покрывала эти комбинации. Иначе говоря, условием отсутствия статических состязаний является связность всех контуров, образуемых на карте Карно при минимизации логической функции.

Для рассмотренного ранее примера

Рис.47. Карта Карно и эквивалентная релейная схема.

В некоторый момент времени контакт уже разомкнется, а контакт x ₁ еще не замкнется, цепь разомкнута.

Для устранения статического риска следует дополнить МДНФ еще одним термом согласования, не изменяющим значения логической функции. На карте Карно ему соответствует дополнительный контур, связывающий контуры. Для рассмотренного примера: __

Y = X1 X2 + X1 X3 + X2 X3.

Рис.48. Карта Карно и релейная схема без состязаний.

Теперь переключение Х1 не вызывает временных изменений Y, так как цепь Х2 Х3 = 1 постоянно, независимо от Х1.

---

Дата добавления: 2015-07-11