Метод карт Карно

Этот метод удобен для минимизации логических функций, содержащих не более 5-6 переменных.

Для минимизации ЛФ приводят к СДНФ и заполняют карту Карно.

Наличие единиц в соседних (по вертикали или по горизонтали) клетках карты соответствует смежным минтермам, которые могут быть склеены. Процесс группировки двух, четырех, восьми и т.д. клеток с единицами удобно проводить визуально, что оформляется в виде прямоугольного контура вокруг этих клеток, после чего можно записать ответ - тупиковую ДНФ в виде дизъюнкции (суммы) простых импликант, описывающих проведенные контуры. При наличии различных вариантов проведения контуров получаем несколько тупиковых ДНФ, среди которых выбираем минимальную.

Пример 1:

__ __

F (X1, X2) = X1·X2 + X1·X2= X1·(X2 + X2) = X1.

Видим, что в импликанте, описывающей контур, остаются те переменные, которые в пределах контура не меняют своего значения.

Правила проведения контуров:

1) внутри контура должны быть только клетки с единицами;

2) количество этих клеток с единицами должно выражаться величиной

2ⁱ (i = 0, 1, 2, 3,...), то есть склеиванию может подвергаться одна клетка (нет склеивания), две клетки (минус одна переменная), четыре клетки

1

(минус две переменных), 8, 16 и т.д.;

3) единицы в крайних клетках одного

столбца или строки могут включаться

в один контур, то есть карту можно

закручивать в трубку по обеим осям;

4) каждый контур должен включать как можно большее число клеток с единицами (2,4,8,..), а общее число контуров должно быть как можно меньшим;

5) каждая клетка может входить в несколько контуров, но каждый контур должен иметь как минимум одну единичную клетку, не входящую в другие контуры (нельзя проводить контур внутри другого контура).

В простую импликанту, описывающую каждый контур, включаются только те переменные, которые во всех клетках контура не меняют своего значения (то есть имеют прямое или инверсное вхождение).

Пример 2 (из метода Квайна). Имеется два варианта проведения контуров.

__ __ __ __ __ __ __

F(X1, X2, X3) = X1·X2·X3 + X1·X2·X3 + X1·X2·X3 + X1·X2·X3 + X1·X2·X3;

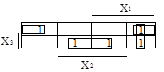
Рис.25. Первый вариант Рис.26. Второй вариант.

Fmin1 = Х2·Х3 + Х2·Х3 + Х1·Х3. Fmin2 = X1·X2 + X2·X3 + X2·X3.

Пример 3: здесь такжевозможны два варианта проведения контуров через

правую нижнюю клетку.

__ __ __ __

а) F = X1·X3·X4+X1·X2·X3+X1·X4+X3·X4;

__ __ __ __ __

б) F = X1·X3·X4+X1·X2·X4+X1·X4+X3·X4.

Рис.27.

Видим, что при 4-х..5-ти переменных метод карт Карно проще метода Квайна, но визуальный метод проведения контуров, легко доступный человеку, плохо поддается алгоритмизации на ЭВМ.

При минимизации частично определенных ЛФ некоторым безразличным значениям функции присваивают значение 1, если это позволяет образовать более крупный контур, остальные считают равными 0. В результате получаем более простое выражение минимальной ЛФ.

Дата добавления: 2015-07-11