Не равным степени двух.

Пример 1. Пусть требуется синтезировать счетчик с модулем счета равным трем. Минимальное число необходимых триггеров - 2 (ближайшее большее число - целая степень двойки - это ).

Нарисуем незаконченную схему счетчика:

Рис.37.

Рассмотрим метод, позволяющий определить, как следует подключить информационные входы триггеров для счета до трех.

Составим таблицу состояний триггеров:

i

Рис.38. Граф переходов счетчика.

Перевод счетчика в следующее состояние связан с переключением триггеров. Составим таблицу переходов JK - триггера:

Вид перехода	J	K
0 0		*
0 1		*
1 0	*
1 1	*

Знак «*» означает, что логический уровень на входе может быть произвольным. Пользуясь этими таблицами, построим таблицы истинности для входов J и K всех триггеров.

При этом логические уровни на входах J и K являются функциями текущего состояния счетчика от Q1, Q2, a Q1 и Q2 есть состояния триггеров перед поступлением на вход триггеров очередного импульса С.

Пусть имеем исходное состояние счетчика Q1 = Q2 = 0.

Под действием входного импульса должно быть обеспечено новое состояние Q2 = 0; Q1 = 1. Следовательно, триггер Т1 должен совершить переход 0 1, требующий на следующих уровнях сигнала на входах J1=1; K1=*. Триггер Т2 совершает переход 0 0, что обеспечивается сигналами на входах J2 = 0; K2 = *. Заносим эти значения в клетки карт Карно, соответствующие текущему состоянию счетчика Q2 = 0; Q1 = 0 (левый верхний угол).

Перевод триггеров из текущего состояния Q2 = 0; Q1 = 1 в следующее состояние Q2 = 1; Q1 = 0 требует подачи на информационные входы следующих сигналов:

-триггер Т1 совершает переход 1 0, для чего необходимы J1 = *; K1 = 1;

-триггер Т2 совершает переход 0 1, следовательно J2 = 1; K2 = *.

Текущее состояние Q2 = 0; Q1 = 1, чему соответствует правый верхний угол карты Карно.

Дальнейший переход: текущее состояние Q2 = 1; Q1 = 0;

следующее - Q2 = 0; Q1 = 0.

Т1: переход 0 0 J1 = 0; K1 = *;

Т2: переход 1 0 J2 = *; K2 = 1;

текущее состояние Q2=1; Q1=0 - левый нижний угол карты Карно.

Состояние Q2 = 1; Q1 = 1 в этом счетчике не используется и объявляется запрещенной комбинацией (Х на карте). Теперь мы имеем заполненные карты Карно для всех входов схемы. Проводим минимизацию логических функций:

__

J1 = Q2; K1 = 1; J2 = Q1; K2 = 1.

Этому соответствует схема счетчика до трех (рис.39).

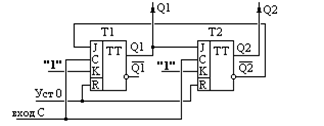
Рис.39. Схема счетчика до 3.

Пример 2. Проведем синтез структуры двоично-десятичного счетчика до десяти. Для N =10 необходимо 4 триггера, так как , но 6 состояний не используются.

Рис.40.Незаконченная схема счетчика.

Таблица состояний и переходов:

Текущее (i-ое)

следущее (i+1)

T4

T3

T2

T1

i

Q4

Q 3

Q 2

Q 1

Q 4

Q 3

Q 2

Q 1

переход

J

K

переход

J

K

переход

J

K

переход

J

K

0

*

*

*

*

1

*

*

*

*

2

*

*

*

*

3

*

*

*

*

4

*

*

*

*

5

*

*

*

*

6

*

*

*

*

7

*

*

*

*

8

*

*

*

*

9

*

*

*

*

0

Рис.41. Схема расположения минтермов (обратите внимание на измененное расположение переменных).

Составляем карты Карно и ищем МДНФ:

__

J1 = 1; K1 = 1; J2 = Q1 Q4;

K2 = Q1; J3 =Q1× Q2; K3 = Q1× Q2;

J4 = Q1× Q2× Q3; K4 = Q1.

В соответствии с полученными уравнениями строим схему счетчика.

Рис.42. Схема счетчика до 10.

Дата добавления: 2015-07-11