Принципы перевода чисел из одной позиционной СС в другую.

2→10

Целые числа: 101101₂=1*2⁵+0*2⁴+1*2³+1*2²+0*2¹+0*2⁰+1=32+0+8+4+0+0+1=45₁₀

Дробные числа: 101,11₂=1*2²+0*2¹+1*2⁰+1*2^-1+1*2^-2=4+0+1+0,5+0,25=5,75₁₀

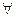→10 (аналогично)

112₃=1*3²+1*3¹+2*3⁰=9+3+2=14₁₀

15FC₁₆=1*16³+5*16²+15*16¹+12=4096+1280+240+12=5628₁₀

10→2

Целые числа:

Способ 1. Нужно суметь разложить десятичное число на слагаемые, содержащие степени 2.

Например, 15₁₀=8+4+2+1=1*2³+1*2²+1*2¹+1=1111₂

Однако большое число, например 157 таким образом перевести в двоичную систему достаточно трудно. Существует другой способ.

Способ 2. Данное десятичное число делится с остатком на основание системы. Полученный остаток – это младший разряд искомого числа, а полученное частное снова делится с остатком, который равен второй справа цифре и т.д. Так продолжается до тех пор, пока частное не станет меньше делителя (основания системы). Это частное – старшая цифра искомого числа.

37 2 а₅ а₄ а₃ а₂ а₁ а₀

36 18 2 37₁₀=100101₂

а₀=1 18 9 2

а₁=0 8 4 2

а₂=1 4 2 2

а₃=0 2 1 = а₅

а₄=0

10→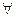

315 8 315₁₀=473₈ 315 16 315₁₀ =13В₁₆, т.к. 11₁₀=В₁₆

24 39 8 16 19 16

75 32 4 = а₂ 155 16 1 = а₂

72 7 = а₁ 144 3 = а₁

а₃ = 3 а₀ = 11

Дробные числа:

Перевод дробного десятичного числа в другую систему счисления производится путем последовательных умножений на основание новой системы с выделением цифр целой части произведений в качестве искомых.

10→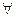

Дано: 0,1875₁₀

0,1875 0,1875 0,1875

^* 2 ^* 8 16

0,3750 1,5000 1,1250

^* 2 ^* 81,875

0,7500 4,0000 3,0000

^* 2

1,5000 0,1875₁₀=0,14₈ 0,1875₁₀=0,3₁₆

^* 2

1,0000

0,1875₁₀= 0,0011₂

Перевести в двоичную СС десятичную дробь 0,79₁₀ с точностью до 3 знаков.

0,79 0,79₁₀=0,110…₂

^* 2

1,58

^* 2

1,16

^* 2

0,32

Таблица соответствия чисел в различных системах счисления

С практической точки зрения представляет интерес процедура взаимного преобразования двоичных, восьмеричных и шестнадцатеричных чисел. Для этого пользуются таблицей «соответствия чисел в различных системах счисления».

Таблица соответствия чисел

		A
		B
		C
		D
		E
		F

Для перевода целого двоичного числа в восьмеричное необходимо разбить число справа налево на группы по 3 цифры (самая левая группа может содержать менее 3х двоичных цифр), а затем каждой группе поставить в соответствие ее восьмеричный эквивалент.

Например, 11011001₂=11`011`001₂=331₈.

Для перевода целого двоичного числа в шестнадцатеричное необходимо разбить число справа налево на группы по 4 цифры (самая левая группа может содержать менее 4х двоичных цифр), а затем каждой группе поставить в соответствие ее шестнадцатеричный эквивалент. Например,

1100011011001₂=1`1000`1101`1001₂=18D9₁₆.

Группу из трех двоичных цифр называют «двоичной триадой», из 4 цифр – «двоичной

тетрадой».

Дата добавления: 2015-07-11