Задачи для самостоятельного решения. 1.Найти координаты вершин, оси, фокусы и эксцентриситет эллипсов:

1.Найти координаты вершин, оси, фокусы и эксцентриситет эллипсов:

а)16х²+25y²=400

б)4x²+9y²=36

в)16x²+9y²=144

г)25x²+9y²=900

Сделать чертежи.

2.Составить уравнение эллипса, зная, что:

а) его большая полуось равна 10 и фокусы F₁(-6;0) F₂(6;0)

б)его малая ось равна 6 и фокусное расстояние равно 8.

Сделать чертежи.

3.В окружность, заданную уравнением x²+y²=10, вписан эллипс, касающийся её концами своей большой оси, при этом а=2в. Найти уравнение эллипса.

4.Дан эллипс x²/169+y²/144=1. Найти фокусное расстояние.

5.Написать уравнение эллипса, если даны фокусное расстояние 2с=8 и эксцентриситет ξ=0.8. Сделать чертеж.

6.Написать уравнение эллипса, если его фокусы имеют координаты (0;±5), а эксцентриситет равен 2/3.

7.Найти точки пересечения эллипса 4x²+9y²=36 с прямыми:

а)2x+3y-6=0

б)y=x-6

Сделать чертежи.

8.Прямая 2x+y-14=0 пересекает эллипс 4x²+y²=100. Найти длину отрезка этой прямой, заключенного внутри эллипса.

9.Написать уравнение эллипса, у которого сумма полуосей равна 36, а расстояние между фокусами, лежащими на оси OY, равно 48.

10.Найти точки пересечения эллипсов x²/36 +y²/3=1 и x²/12+y²/4=1.

11.Дан эллипс 16x²+25y²=400 и окружность с центром в верхней вершине малой оси эллипса, проходящая через его фокусы. Найти точки пересечения эллипса и окружности.

12.Расстояние между фокусами эллипса равно расстоянию между вершинами большой и малой осей. Найти эксцентриситет эллипса.

13.Малая полуось эллипса, расположенная на оси OY, равно 3 √2, а эксцентриситет ξ= √2/2. Составить уравнение эллипса и найти координаты его фокусов.

14.Составить уравнение эллипса, если один из его фокусов находится в точке (6;0_, а эксцентриситет ξ=2/3.

Гипербола

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой же плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Обозначим фокусы через F₁ (-C;0) и F₂ (C;0) => расстояние между фокусами F₁F₂= 2С - Ф окусное расстояние.

Чертеж

Модуль разности расстояний от каждой точки гиперболы до фокусов 2а

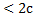=> 2а => а

По определению гиперболы

| MF1 –MF2 | = 2a

MF1 –MF2 = 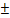2a

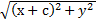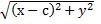- = 2а

После упрощений, аналогичных выводу уравнения эллипса, получим:

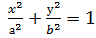, где b²= c²-a²

Дата добавления: 2015-07-11