Читайте также:
|
Каноническое уравнение окружности с центром в точке (x0;y0) и радиусом R.
Если x0= 0; y0= 0 => X2+y2= R2
Уравнение окружности с центром в точке (0;0) и радиусом R.
(рис.)
Задачи
Задача1.
Составить уравнение окружности с центром в точке (2;-3) и радиусом 4 единицы. Выполнить чертёж.
Решение:
В уравнение окружности: (х - х0)2 + (у - у0)2 = R2
Подставим координаты центра x0 = 2; y0 = -3 и R = 4.
(x - 2)2 + (y + 3)2 = 16
(рис.)
Задача2.
По уравнению окружности х2 - 2х + у2 + 4у – 4 = 0 найти координаты центра и радиус окружности. Выполнить чертеж.
Решение:
х2 - 2х + у2 + 4у – 4 = 0
Дополним суммы х2 - 2х и у2 + 4у до квадратов. Для этого прибавим к первой сумме 1, ко второй 4, затем их вычтем, получим:
х2 - 2х + 1 + у2 + 4у + 4 - 4 - 1 – 4 = 0
(х - 1)2 + (у + 2)2 = 9
Центр окружности (1;-2); R=3.
(рис.)
Контрольные вопросы:
1.Что называется окружностью?
2.Записать каноническое уравнение окружности и поясните значения неизвестных в нем.
3.Записать уравнение окружности с центром в начале координат.
4.Составить каноническое уравнение окружности с центром в точке С(-3;1) и радиусом R=2
Задачи для самостоятельного решения.
1. Составьте каноническое уравнение окружности, если её:
а)Центр в точке С(о; в) и радиус R
б)Центр в точке С(а; о) и радиус R
в)Центр в точке С(о; -в) и радиус R
г)Центр в точке С(-а; о) и радиус R
Сделать схематический чертеж, если а>0,в>0.
2. Составить уравнение окружности с данным центром и радиусом.
а) С(-2; -3); R=1
б)С(-1; 5); R= √3
в)М0(6; -2); R=0,5
г)М0(4; 3); R= ¾
3.Доказать, что уравнение х2+y2-2х+4y-4=0 является уравнением окружности.
Найти её центр и радиус. Сделать чертеж.
4.Для указанных окружностей определить координаты центра М0 и радиус:
а) х2+y2-8x+12y-29=0
б)х2+y2+16x-20y-5=0
в)x2+y2-7y-18=0
г)2x2+2y2-12x-7=0
д)4x2+4y2+16x-32y-41=0
е)9x2+9y2-72x+18y-208=0
И выполнить чертеж.
5.Найти точки пересечения с осями координат каждой из окружностей:
а)x2+y2+4x+4y+3=0
б)x2+y2 + 6x+11y+10=0
6.Найти точки пересечения прямой x-y+1=0 с окружностью x2+y2-4x+16Y-5=0.
7.Дана окружность x2+y2-4x+2y-15=0 и прямая x+y-7=0.
Найти длину хорды, принадлежащей данной прямой.
8.Дана окружность (х-3)2+(y+5)2=16. Лежат ли на ней точки:
а)А(3; -1);
б)В(3; -9);
в)С(0; -3)?
9.Написать уравнение окружности с центром в точке О1, проходящей через точку А,
если даны:
1)О1(2; 1); А(5;5);
2)О1(-3; 2);А(-4;0).
10.Найти расстояние между центрами окружностей x2+y2=16 и x2+y2-12х+11=0.
Сделать чертеж.
11.Даны окружности x2+y2-6x+8x=0 и x2+y2+2x-2y+1=0.
Написать уравнение прямой, проходящей через их центры. Сделать чертеж.
12.Найти точки пересечения окружности (x-2) 2+(y+3) 2=20 и прямой y=x-3.
Сделать чертеж.
Эллипс
Эллипсом называется множество всех точек, плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. (F1 и F2)
F1M1+F2M1=F1M2+F2M2=F1M3+F2M3=Const>F1F2
Выберем систему координат XОY так, чтобы фокусы F1и F2 лежали на оси OX, а начало, координат совпало со серединой F1F2.
Обозначим фокусы через F1 и F2, расстояние F1F2 через 2С; сумму расстояний от M- точки эллипса до фокусов.
MF1 + MF2 через 2a => 2a > 2c
a > c
MF1 + MF2 = 2a
+ 
=2a
+ 
= 2a
Преобразуем:
(x2+c2)+y2 = (2a )2
x2 + 2xc + c2 + y2 = 4a2 - 4a + x2 -2xc + c2 + y2
a = a2 - cx
a2x2 - 2a2xc + a2c2 + a2y2 = a4 – 2a2cx + c2x2
(a2 - c2)x2 + a2y2 = a2(a2 - c2)
Т.к. a > c => a2 – c2 > 0
Обозначим a2 – c2 = b2
Тогда b2x2 + a2y2 = a2b2 или 
, где a2 – c2 = b2
Каноническое уравнение эллипса
Эллипс – кривая второго порядка.
Исследование формы эллипса по его уравнению
Т.к уравнение содержит x и y только в чётных степенях =>
точки 
принадлежат эллипсу =>
=> Эллипс симметричен относительно осей Ox и Oy, а также относительно точки O(0;0), которую называют центром эллипса.
Найдём точки пересечения эллипса с осями координат.
С осью Оx: пусть y=0 => 
= 
1,2 = 
a =>
=> Эллипс пересекает ось Оx в точках A1 (-a;0); A2 (a;0)
С осью Оy: пусть x=0 =>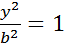 
= 
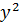1,2 = b =>
=> Эллипс пересекает ось Оy в точках B1 (-b;0); B2 (b;0)
(Рис.)
Точки A1;A2;B1;B2 называются вершинами эллипса
Отрезок А1А2= 2а – большая ось эллипса
Отрезок B1B2= 2b – малая ось эллипса
Число а – большая полуось
Число b – большая полуось
Т.к.
= =
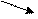
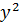
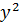1,2 = a 1,2 = b
(Рис.) (Рис.)
-а 
-b 
Þ Все точки эллипса лежат внутри прямоугольника,
ограниченного прямыми
x=-a; x=a; y=-b; y=b
Т.к. => Чем больше 
, тем меньше 
и наоборот.
Þ если 
возрастает =>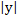 
убывает и наоборот.
Þ Эллипс имеет форму овальной замкнутой кривой.
Определение: отношение фокусного расстояния к большой оси называется ЭКСЦЕНТРИСИТЕТОМ эллипса и обозначается буквой 
(«эпсилон»): 
Т.к. 0 < c < a => 0 ≤ 
< 1
Т.к. 
=> a=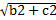 
= 
= 
определяет форму эллипса:
- чем меньше ( →0) => тем более округлый эллипс
- чем больше 
( → 1) => тем более сжат эллипс
- при =0 => эллипс превращается в окружность.
Если в уравнении a 
=> b – большая полуось
а – малая полуось
=> 2b = B1B2 – большая ось на оси Оу
2а = А1А2 – малая ось на оси Ох
фокусы F1(0;-c); F2(0;c) на оси Оу
=> c2=b2-a2 => 
(Рис.)
Задача:
Найти оси, вершины, фокусы, эксцентриситет эллипса 9x2+25y2-225=0
Решение:
Приведём уравнение к каноническому виду:
9x2+25y2=225 |:225
;
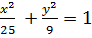
а=5; b=3
Оси эллипса 2a=10; 2b=6
Вершины A1(-5;0); A2(5;0)
B1(0;-3); B2(0;3)
c2= a2- b2 => c = 
= 
= 4
Фокусы: F1(-4;0); F2(4;0)
Эксцентриситет: 
Чертеж (задача к эллипсу)**
Контрольные вопросы
1.Что называется эллипсом?
2.Записать каноническое уравнение эллипса, пояснить значения а и в.
3.Записать координаты фокусов, вершин эллипса.
4.Что называется большой и малой осью эллипса?
5.Дать определение эксцентриситета эллипса. Записать формулу.
6.Что характеризует эксцентриситет?
7.Какова величина эксцентриситета эллипса?
Дата добавления: 2015-07-11; просмотров: 374 | Нарушение авторских прав