
Читайте также:
|
Рассмотрим полярную систему координат на плоскости. Пусть нам задан полюс и полярная ось. Для произвольной точки  на плоскости обозначим через
на плоскости обозначим через 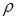 расстояние от точки
расстояние от точки  до точки
до точки  , а через
, а через 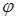 – угол, на который нужно повернуть полярную ось до совмещения с лучом.
– угол, на который нужно повернуть полярную ось до совмещения с лучом.
 |
Рис. 22.
Числа 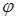 ,
, 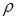 называются полярными координатами точки
называются полярными координатами точки  . Число
. Число 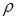 называют полярным радиусом (всегда
называют полярным радиусом (всегда  ), а число
), а число 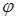 называют полярным углом точки
называют полярным углом точки  . Полярный радиус для любой точки определяется однозначно, а полярный угол – с точностью до
. Полярный радиус для любой точки определяется однозначно, а полярный угол – с точностью до  , где
, где  – целое число.
– целое число.
Пусть на плоскости задана полярная и правая декартова прямоугольная система координат.
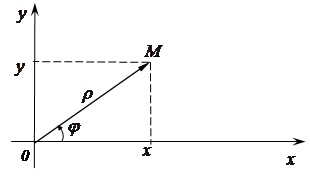 |
Рис. 23.
Пусть  – произвольная точка плоскости, имеющая декартовы координаты
– произвольная точка плоскости, имеющая декартовы координаты  и полярные координаты
и полярные координаты 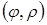 . Рассмотрим радиус вектор
. Рассмотрим радиус вектор  точки
точки  . Сравнивая координаты, получим формулы перехода от декартовых координат к полярным:
. Сравнивая координаты, получим формулы перехода от декартовых координат к полярным:
 ,
,  .
.
Формулы перехода от полярных координат  к декартовым
к декартовым  можно записать в виде:
можно записать в виде:
 ,
, 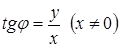 .
.
При  можно вычислить
можно вычислить 
 .
.
Кривую в полярных координатах задают в виде уравнения  или явного уравнения в виде
или явного уравнения в виде  .
.
Рассмотрим несколько примеров кривых, заданных в полярных координатах.
1. Уравнение 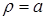 , где
, где 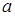 – постоянное число, задает окружность радиуса
– постоянное число, задает окружность радиуса 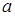 , центр которой совпадает с полюсом
, центр которой совпадает с полюсом  .
.
2. Уравнение  определяет луч, исходящий из полюса и составляющий угол
определяет луч, исходящий из полюса и составляющий угол 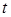 с полярной осью.
с полярной осью. 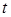 – произвольное число.
– произвольное число.
3. Выведем полярное уравнение окружности радиуса 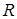 в случае, когда полюс лежит на ней, а полярная ось проходит через центр окружности.
в случае, когда полюс лежит на ней, а полярная ось проходит через центр окружности.

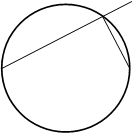
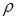


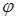



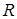
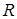

Рис. 24.
Возьмем произвольную точку  на окружности. Треугольник
на окружности. Треугольник  прямоугольный. Получаем уравнение окружности в виде
прямоугольный. Получаем уравнение окружности в виде  .
.
4. Покажем, что уравнение  и полярных координатах определяет окружность радиуса
и полярных координатах определяет окружность радиуса 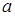 . Подставим выражения для
. Подставим выражения для 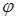 и
и 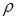 через
через  и
и 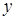 в уравнение:
в уравнение:  . Умножая обе части уравнения на
. Умножая обе части уравнения на  , получим
, получим  или
или 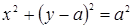 . Это уравнение окружности радиуса
. Это уравнение окружности радиуса  с центром в точке
с центром в точке  .
.
5. Пусть в декартовой системе координат заданы прямые  ,
,  . Уравнения этих прямых в полярной системе координат
. Уравнения этих прямых в полярной системе координат  ,
, 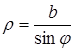 .
.
6. Рассмотрим уравнение  ,
, 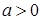 . Переход к декартовым координатам здесь довольно громоздкий и приводит к алгебраическому уравнению высокой степени. Поэтому посмотрим эту кривую, исходя из качественных соображений.
. Переход к декартовым координатам здесь довольно громоздкий и приводит к алгебраическому уравнению высокой степени. Поэтому посмотрим эту кривую, исходя из качественных соображений.
Период правой части уравнения равен 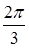 , поэтому достаточно построить кривую для значений полярного угла из интервала
, поэтому достаточно построить кривую для значений полярного угла из интервала  . По свойствам функции
. По свойствам функции  , см. рис. 22, видно, что полярный радиус
, см. рис. 22, видно, что полярный радиус 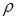 монотонно возрастает при
монотонно возрастает при  и при
и при  монотонно убывает. При
монотонно убывает. При 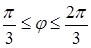 правая часть уравнения
правая часть уравнения  отрицательна, для этих значений
отрицательна, для этих значений 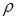 точек кривой нет. Для остальных значений кривая получается при повороте на угол
точек кривой нет. Для остальных значений кривая получается при повороте на угол 
 части кривой, расположенной между лучами
части кривой, расположенной между лучами  и
и  , рис. 24.
, рис. 24.
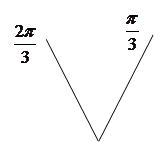 | |||||
 | |||||
| |||||



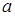
 | |||
 | |||
|












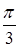

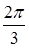
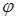

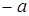
Рис. 25.
Дата добавления: 2015-07-11; просмотров: 184 | Нарушение авторских прав