Параметрическое задание кривых на плоскости.

Пусть заданы две функции одного аргумента

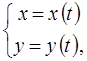(17)

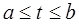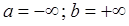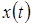где (в частности допускается ). При каждом значении числа и 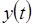будем понимать как координаты некоторой точки на плоскости, причем эта точка, вообще говоря, меняется вместе с изменением , описывая некоторую кривую 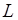. В этом случае систему уравнений (17) называют параметрическими уравнениями линии , а аргумент называют параметром.

Переход от параметрических уравнений к уравнению 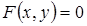осуществляется исключением параметра 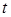из системы уравнений (17).

Рассмотрим несколько примеров.

1. 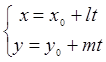– известные параметрические уравнения прямой, проходящей через точку 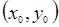с направляющим вектором , .

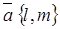2. 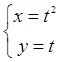. Исключая параметр 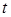, получаем 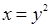, то есть уравнение параболы, .

3. Уравнения 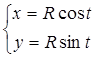– уравнения окружности радиуса 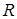, т.к. , .

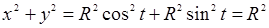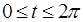4. Уравнения 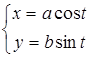, 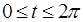– являются параметрическими уравнениями эллипса.

5. Циклоида.

Пусть по прямой без скольжения катится круг радиуса . Кривая, описываемая фиксированной точкой круга, называется циклоидой. Уравнения циклоиды .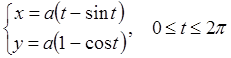

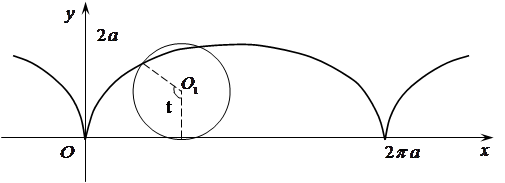Рис. 19.

6. Астроида.

Пусть по окружности радиуса 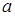внутри нее катится без скольжения круг радиуса 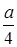. Траектория, которую описывает фиксированная точка, лежащая на границе подвижного круга, называется астроидой.

O

x

a

- а

Рис. 20.

Уравнения астроиды , .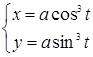

7. Кардиоида.

Пусть по окружности радиуса 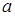вне ее катится без скольжения круг того же радиуса 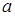. Кривая, которую описывает фиксированная точка подвижного круга, называется кардиоидой.

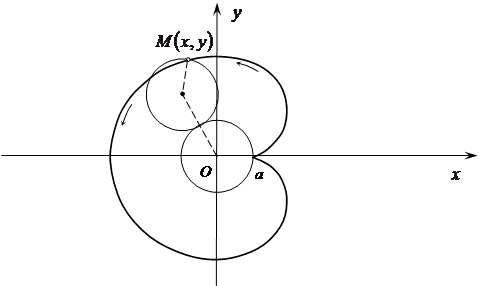Рис. 21.

Уравнения кардиоиды , .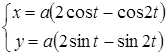

Дата добавления: 2015-07-11