Задание. 1. В тригонометрических функциях часто используется число

1. В тригонометрических функциях часто используется число . Ведите в ячейке А3 формулу =ПИ() и нажмите Enter. Результат равен 3,141592654.

Обратите внимание на отсутствие аргумента (некоторые функции не имеют аргументов, но должны все равно содержать круглые скобки).

2. Перевод градуса в радианы осуществляется с помощью функции РАДИАНЫ.

Например, 60⁰ это . Установите курсор в ячейку A4 и введите формулу =радианы(60). Результат равен числу 1,047197551, которое в свою очередь и есть 3,141592654 деленное на 3.

Для перевода угла в градусы используется ГРАДУСЫ.

В ячейке В4 результатом формулы =градусы(пи()/4) является число, равное 45.

В ячейке С4 запишите =градусы(пи()), в результате числовое значение изображается в градусах.

1. Найдем cos угла различными способами (формулы вводить в Е1, Е2,Е3 соответственно):

1) =cos(пи()/4)

В данном случае использовали функцию пи().

2) Не всегда градусы можно выразить через . Например cos23⁰ находится по формуле:

=cos(радианы(23))

В данном случае сначала 23⁰ переводятся в радианы, а затем вычисляется cos, т.е приоритет внутренних скобок.

3) Или по формуле =cos(23*пи()/180)

В данном случае использовали формулу перевода градуса в

радианы

2. Обратите внимание, что вместо числовых значений лучше использовать адреса ячеек. Например,

Такой вариант предусматривает изменение значения аргумента и автоматический перерасчет значения функции.

С помощью вставки функций рассмотрите синтаксис тригонометрических функций cos, sin, tg, ctg

1) SIN(аргумент в радианах) – для нахождения синуса угла

2) COS(аргумент в радианах) – для нахождения косинуса угла

3) TAN(аргумент в радианах) – для нахождения тангенса угла

4) Котангенс находится по формуле 1/TAN(аргумент в радианах)

Задание на закрепление. Составьте таблицу 1 на 2 листе и по аналогии со столбцом В заполните всю таблицу

Вывод. При нахождении тригонометрической функции аргумента используются формулы:

=sin(радианы())

=cos(радианы()) где - угол в градусах

=tan(радианы())

- Рассмотрим обратные тригонометрические функции на примере вычисления arcsin1.

Введите в ячейку Е4 на 1 листе формулу =asin(1), результатом будет число 1,570796327, а это и есть /2 или 90⁰. Чтобы результат показать в привычной форме, необходимо перевести полученный ответ в градусы по формуле =градусы(asin(1)).

Задание на закрепление. Самостоятельно заполните таблицу 2 на 2 листе

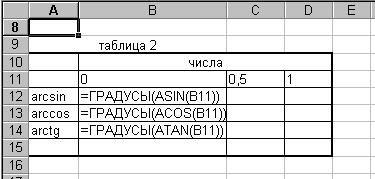
1) ASIN – для нахождения arcsin

2) ACOS – для нахождения arccos

3) ATAN –для нахождения arctg

Вывод. При нахождении обратных тригонометрической функции используются формулы:

=градусы(аsin(а))

=градусы(асоs(а)) где а - число

=градусы(атаn(а))

Задание. Часто в Excel используются некоторые статистические функции.

Перейдите на лист 3, заполните в соответствии с рисунком содержимое ячеек, и введите формулы:

в B11 =срзнач(B1:B10)

в B12 =макс(B1:B10),

в B13 =мин(B1:B10).

Сделайте анализ полученных результатов.

Дата добавления: 2015-07-11