
Сплайн кусковий поліном ступеня K з безперервною похідною ступеня K-1 в точках з'єднання сегментів.
Далі будемо розглядати кубічні сплайни.
Поняття сплайна прийшло з машинобудування, де сплайном називали гнучку лінійку, закріпивши яку в потрібних місцях, добивалися плавної кривої, яку потім креслили по цій лінійці (див. рис. 4).
Форма такої лінійки, якщо її розглядати як функцію у(x), задовольнятиме рівнянню Эйлера-Бернуллі: 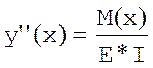 , де M(x) - момент вигину уздовж рейки, E - модуль Юнга, залежний від властивостей матеріалу рейки, I - момент інерції, визначуваний формою кривої. Якщо ми фіксуємо деякі точки підпорами, то момент вигину на кожному відрізку
, де M(x) - момент вигину уздовж рейки, E - модуль Юнга, залежний від властивостей матеріалу рейки, I - момент інерції, визначуваний формою кривої. Якщо ми фіксуємо деякі точки підпорами, то момент вигину на кожному відрізку 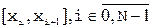 змінюється за лінійним законом: M(x) = A*x + B, підставляючи в початкове рівняння одержуємо:
змінюється за лінійним законом: M(x) = A*x + B, підставляючи в початкове рівняння одержуємо:
 , двічі інтегруючи одержуємо рівняння кривої на даному відрізку:
, двічі інтегруючи одержуємо рівняння кривої на даному відрізку:
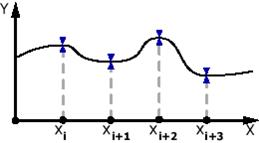 Рис. 4. Сплайн.
Рис. 4. Сплайн.
| 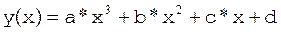 ;
таким чином форма фізичного сплайна описується шматковим кубічним поліномом.
Розглянемо завдання побудови системи таких кубічних поліномів для всього відрізка ;
таким чином форма фізичного сплайна описується шматковим кубічним поліномом.
Розглянемо завдання побудови системи таких кубічних поліномів для всього відрізка 
|
1) Для N відрізків маємо 4N коефіцієнтів:  для
для 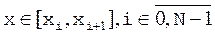 ;
;
2) Умова 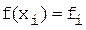 (i Î
(i Î 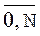 ) дає 2N рівнянь;
) дає 2N рівнянь;
3) Вимога  в точках
в точках 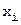 (i Î
(i Î 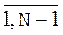 ) дає N-1 рівняння;
) дає N-1 рівняння;
4) Вимога  в точках
в точках 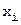 (i Î
(i Î  ) дає N-1 рівнянь.
) дає N-1 рівнянь.
Всього маємо 4N-2 рівнянь; для того щоб система була визначеною, необхідно ще 2 рівняння; їх можна вивести, наприклад, із заданих значень похідних на граничних точках або із умови періодичності. При коректно заданих умовах лінійна відносно 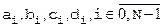 система має єдинее рішенння.
система має єдинее рішенння.
Усі форми реалізуються параметоричним методом. Якщо  - незалежний параметр, такий що
- незалежний параметр, такий що  . Кубічним параметричним сплайном називають наступну систему рівнянь:
. Кубічним параметричним сплайном називають наступну систему рівнянь:

Ермітова матриця
 .
.
де  - ермітова матриця,
- ермітова матриця,  - геометричний вектор Ерміта.
- геометричний вектор Ерміта.
 .
.
 ,
,
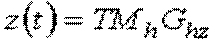
3. Апроксимація
3.1. Криві Безьє
Для задач апроксимації найширше застосовуються криві Безье. Це пов'язано з їх зручністю як для аналітичного опису, так і для наочної геометричної побудови (стосовно комп'ютерної графіки це означає, що користувач може задавати форму кривої інтерактивно, тобто рухаючи опорні точки курсором на екрані).
Наочний метод побудови цих кривих був запропонований de Casteljau в 1959 році. Побудуємо криву по 3 опорним точкам (Мал. 5). Метод de Casteljau заснований на розбитті відрізків, що сполучають початкові точки відносно t (значення параметра), а потім в рекурсивному повторенні цього процесу для одержаних відрізків.
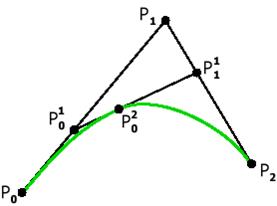 Рис. 5. Крива Безьє з трьома опорними точками
Рис. 5. Крива Безьє з трьома опорними точками
|  Позначимо опорні точки як
Позначимо опорні точки як  , ,  , початок кривої в точці , початок кривої в точці  (t=0), а кінець в точці (t=0), а кінець в точці  (t=1), для кожного (t=1), для кожного  найдем точку найдем точку 


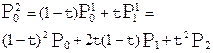 ,
таким чином, отримаємо криву другого порядку. ,
таким чином, отримаємо криву другого порядку.
|
Аналогічно побудуємо криву Безьє з 4 опорними точками.
 Рис. 6. Крива Безьє з 4 опорними точками
Рис. 6. Крива Безьє з 4 опорними точками
| 


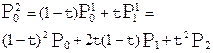
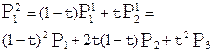
|
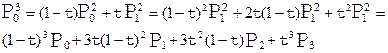
Можно продолжать подобные построения и для большего числа узлов, получая аналогичные выкладки. Запишем общее аналитическое представление для кривой Безье с N+1 опорной точкой:
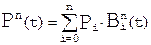 , где
, где  , где
, где 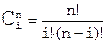 - биномиальные коэффициенты,
- биномиальные коэффициенты,
 называются базисными многочленами Бернштейна n степени (а также весовыми функциями Безье/Бернштейна). На рисунках ниже изображены многочлены Бернштейна 3 и 4 степеней
называются базисными многочленами Бернштейна n степени (а также весовыми функциями Безье/Бернштейна). На рисунках ниже изображены многочлены Бернштейна 3 и 4 степеней


Дата добавления: 2015-07-11; просмотров: 192 | Нарушение авторских прав