
Читайте также:
|
1. Апроксимація та інтерполяція.
У цій лекції розглядатимуться питання побудови кривих по контрольних точках. Нас цікавитимуть два завдання:
Інтерполяція -побудова кривої, що проходить через контрольні точки
Апроксимація -наближення кривої (не обов'язково проходить точно через задані точки, але задовольняє деякій заданій властивості щодо цих точок)
2. Інтерполяція
Загальна постановка задачі:
 Рис. 1. Постановка завдання
Рис. 1. Постановка завдання
| Дано:
 . . 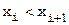 i Î i Î  .
Побудувати функцію f(x), що задовольняє цій умові. .
Побудувати функцію f(x), що задовольняє цій умові.
|
2.1. Інтерполяційний многочлен Лагранжа
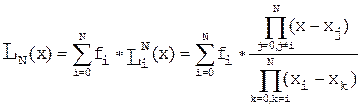 ;
;
 ;
; 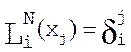
Одержуємо безперервну функцію, що проходить через всі точки
Недоліки:
1) Вимагає значних обсягів обчислень для знаходження значення функції в довільній точці.
2) Невизначена поведінка побудованої функції між вузлами, зокрема можна привести наступні результати:
1916 Бернштейн: 


1925 Рунге: 


Далі розглядатимемо інтерполяційні функції, які задаються окремо на кожному відрізку  , що дозволяє краще враховувати локальну поведінку необхідної функції і уникнути громіздких обчислень (оскільки на кожному з відрізків інтерполююча функція має по можливості простий вигляд).
, що дозволяє краще враховувати локальну поведінку необхідної функції і уникнути громіздких обчислень (оскільки на кожному з відрізків інтерполююча функція має по можливості простий вигляд).
2.2. Кусково-лінійна інтерполяція
 Рис. 2. Кусково-лінійна інтерполяція
Рис. 2. Кусково-лінійна інтерполяція
|  Интерполяция следующей кусочно-линейной функцией: Интерполяция следующей кусочно-линейной функцией:
 Клас
Клас 
|
2.3. Кубічна інтерполяція Ерміта (форма Ерміта)
 Рис. 3. Кубічна інтерполяція Ерміта.
Рис. 3. Кубічна інтерполяція Ерміта.
| Задано наступні умови:
 , , 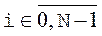
|
Для кожного i шукатимемо функцію у вигляді
 .
Підставивши цю функцію в рівняння умов одержимо лінійну невироджену систему з 4 рівнянь з 4 невідомими (а, b, c та d), тобто рішення існує і єдино.
Клас .
Підставивши цю функцію в рівняння умов одержимо лінійну невироджену систему з 4 рівнянь з 4 невідомими (а, b, c та d), тобто рішення існує і єдино.
Клас 
|
Эта система решается относительно  нахождением обратной матрицы размером
нахождением обратной матрицы размером  .
.
 .
.
Здесь  - эрмитова матрица,
- эрмитова матрица,  - геометрический вектор Эрмита. Подставим выражение
- геометрический вектор Эрмита. Подставим выражение  для нахождения
для нахождения  :
:  . Аналогично для остальных координат:
. Аналогично для остальных координат:  ,
, 
Проблеми:
1) Необхідно знати вектори похідних (напрям + значення)
2) Бажано мати  , а не тільки
, а не тільки 
Дата добавления: 2015-07-11; просмотров: 112 | Нарушение авторских прав