
Читайте также:
|
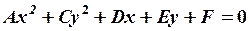 .(7)
.(7)
Такой вид уравнения определяет кривую, оси симметрии которой параллельны осям координат 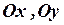 (или, в случае нецентральной кривой, ось симметрии параллельна одной из осей). Выбрав в качестве новых осей координат оси симметрии, или осуществив параллельный перенос системы координат, уравнение (7) может быть приведено к каноническому виду.
(или, в случае нецентральной кривой, ось симметрии параллельна одной из осей). Выбрав в качестве новых осей координат оси симметрии, или осуществив параллельный перенос системы координат, уравнение (7) может быть приведено к каноническому виду.
Известно также, что 1) если 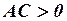 , то уравнение (7) определяет кривую эллиптического типа; 2) если
, то уравнение (7) определяет кривую эллиптического типа; 2) если 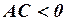 , то гиперболического; 3) если
, то гиперболического; 3) если 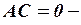 параболического.
параболического.
Первый способ решения задания 2 а).
Линия второго порядка задана уравнением
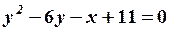 .
.
В этом уравнении 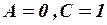 . Так как
. Так как 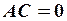 , то данная линия – параболического типа. Путем параллельного переноса системы координат приведем уравнение к виду
, то данная линия – параболического типа. Путем параллельного переноса системы координат приведем уравнение к виду 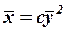 . Подставим вместо
. Подставим вместо 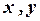 их выражения через
их выражения через 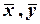 по формулам (2):
по формулам (2): 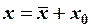 ,
, 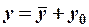 , получим
, получим
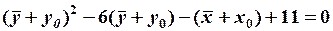 , или
, или
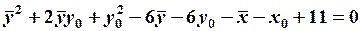 , или
, или
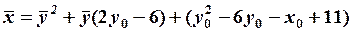 .(8)
.(8)
Подберем 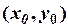 так, чтобы слагаемое с
так, чтобы слагаемое с 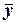 и свободный член обратились в нуль, т.е. полагая
и свободный член обратились в нуль, т.е. полагая 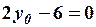 ,
, 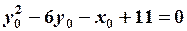 , найдем
, найдем 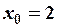 ,
, 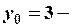 координаты нового начала
координаты нового начала 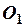 . Найденные значения
. Найденные значения 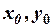 подставим в уравнение (8), получим
подставим в уравнение (8), получим 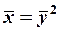 .
.
Построим системы координат 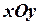 (данную) и
(данную) и 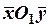 . Уравнение
. Уравнение 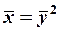 в системе координат
в системе координат 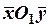 определяет параболу с вершиной в точке
определяет параболу с вершиной в точке 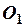 и осью симметрии
и осью симметрии 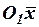 (рис.4).
(рис.4).
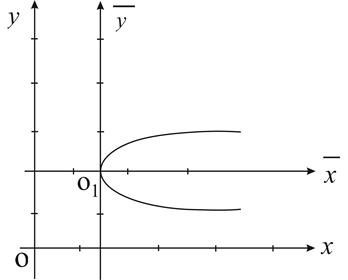
Рис. 4
Второй способ решения задания 2 а).
Возьмем то же уравнение
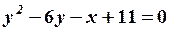
и разрешим его относительно 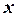 :
: 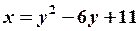 .
.
Выделим полный квадрат относительно 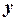
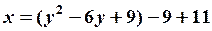 , или
, или 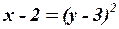 .
.
Таким образом, имеем уравнение параболы с вершиной в точке, координаты которой 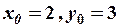 . Поместим начало новой системы координат в вершину параболы, в точку
. Поместим начало новой системы координат в вершину параболы, в точку 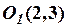 , и выполним параллельный перенос осей координат, используя формулы
, и выполним параллельный перенос осей координат, используя формулы
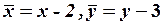 ,
,
тогда уравнение данной параболы в системе 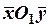 (см. рис.4) будет
(см. рис.4) будет 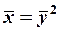 .
.
Решение задания 2 б).
Дано уравнение
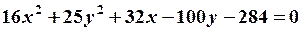 .
.
Так как 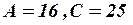 ,
, 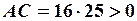 , то уравнение определяет кривую эллиптического типа. Приведем уравнение к каноническому виду. Сгруппируем слагаемые с
, то уравнение определяет кривую эллиптического типа. Приведем уравнение к каноническому виду. Сгруппируем слагаемые с 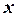 и слагаемые с
и слагаемые с 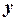
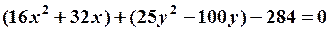 , или
, или
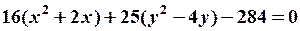 ,
,
выделим полный квадрат относительно 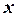 и
и 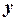
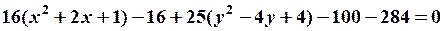 , или
, или
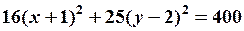 ,
,
окончательно имеем
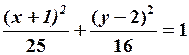 .
.
Перенесем начало координат 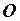 в точку
в точку 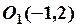 и воспользуемся формулами параллельного переноса системы координат
и воспользуемся формулами параллельного переноса системы координат
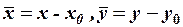 ,
,
или, учитывая координаты выбранного начала,
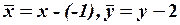 ,
,
тогда уравнение данного эллипса в системе 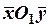 будет выглядеть так:
будет выглядеть так:
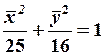 .
.
Построим обе системы координат и эллипс.
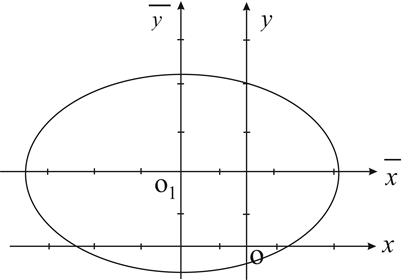
Рис. 5
Решение задания 3.
Дата добавления: 2015-07-11; просмотров: 54 | Нарушение авторских прав