Задания для самостоятельной работы

1. Ток протекает по резистору 10 ом, сопротивление задано с точностью 10%. Ток равен . Согласно закону Ома, падение напряжения на резисторе равно произведению тока на сопротивление. Какова относительная и абсолютная ошибки вычисленного значения напряжения? Ошибками округления пренебречь.

2. Средняя длина авиалинии от Нью-Йорка до Сан-Франциско равняется 2700 милям, но может быть на 200 миль короче или длиннее в результате вариаций маршрута самолета. Средняя скорость самолета на этой линии составляет 580 миль в час, но может оказаться на 60 миль в час больше или меньше из-за ветра. Каковы верхний и нижний пределы времени полета?

3. Реактивное сопротивление емкости дается формулой , где — реактивное сопротивление емкости в Омах, 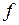— частота в герцах, — емкость в фарадах. Указать границы возможных значений для и

4. Положение свободно падающего тела в вакууме дается формулой , где — ускорение свободного падения в , 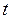— время, прошедшее с начала падения в 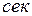. Предположим, что точно, но время может быть измерено с точностью до 0,1 сек. Покажите, что с ростом 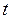абсолютная ошибка вычисленного значения увеличивается, но относительная ошибка — уменьшается.

5. Вычислить значение функции u и ее предельные абсолютную и относительную погрешности, если известны погрешности ее аргументов. Найти количество верных значащих цифр функции u (в широком и узком смысле). Параметры m и n заданы точно. Данные брать из табл.1.3.

Таблица 1.3.

№	u	x	y	m	k
1)	m sin(x+ ky)	3,15 ± 0,02	1,15 ± 5%		1,5
2)	m sin x + cos(1 + ky)	1,25 ± 0,002	1,26 ± 10%		1,6
3)	x^m + y^k	1,23 ± 0,02	1,58 ± 5%		1,7
4)	sin(x – m) + cos ky	1,12 ± 0,01	1,28 ± 2%		1,8
5)	(x^m + y^k)^– 1	1,32 ± 0,01	1,97 ± 2%		1,9
6)	ln(mx + ky)	3,56 ± 0,04	2,56 ± 2%		2,1
7)	mx ^2 + ky ^2	1,84 ± 0,04	6,21 ± 2%		2,2
8)	log2(mx + ky)	5,12 ± 0,02	1,01 ± 2%		2,3
9)	(x ^2 – m + ky ^– 2)	3,44 ± 0,02	1,21 ± 3%		2,4
10)	cos(mx + ky)	4,11 ± 0,02	1,06 ± 4%		2,5
11)	m e ^x+ k e ^– y	1,32 ± 0,02	1,12 ± 5%		2,7
12)	e^mx + ky	2,12 ± 0,02	1,52 ± 6%		2,9
13)	cos(xm + ky)	2,11 ± 0,02	1,1 ± 10%		2,5
14)	3^mx + 2^ky	1,54 ± 0,002	1,5 ± 8%		2,6
15)	m (x ^2 + ky ^2)	1,12 ± 0,02	1,6 ± 2%		2,7
16)	3^mx ∙ 2^ky	1,22 ± 0,02	1,9 ± 2%		2,8
17)	tg(mx – ky)	0,42 ± 0,02	0,14 ± 2%		0,2
18)	lg(mx – ky)	1,45 ± 0,002	1,5 ± 2%		0,1
19)	m^x+ k e ^– y	1,22 ± 0,02	0,1 ± 1%		3,5
20)	m e ^x+ k ^– y	0,52 ± 0,004	2 ± 5%		3,4

6. Опытным путем определить наименьшее значение с плавающей точкой, наибольшее значение и относительную погрешность представления числа для программы Калькулятор в Windows.

Дата добавления: 2015-07-11