|
Читайте также: |
Пусть задана произвольная функция u = f (x 1, x 2, …, xn), где x 1, x 2, …, xn — приближенные величины, а 
— их известные предельные абсолютные погрешности. Тогда предельная абсолютная погрешность результата — функции u — для малых 
вычисляется по формуле [7]:
(1.17)
Как видно из формулы (1.17), для ее применения требуется, чтобы функция f (x 1, x 2, …, xn) была дифференцируемой по всем переменным.
Пример 1.17. Вычислить функцию 
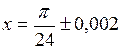, если 
и 
. Найти предельные абсолютную и относительную погрешности результата и определить число верных значащих цифр.
Решение. Применяя формулу (1.17), имеем
Для функции u находим 
. Учитывая предельную абсолютную погрешность D u ≈ 0,04, получаем, что результат имеет две верные значащие цифры в узком смысле. Ответ можно записать в виде u = 1,4 ± 0,04.
Дата добавления: 2015-07-11; просмотров: 107 | Нарушение авторских прав