Распределение ошибки измерений общего показателя теста Векслера

Показатели О. и. имеют большое зна­чение при оценке надежности методики. Надежность теста можно выразить в виде стандартной О. и. (σ_m), называемой также стандартной ошибкой показателя. При интерпретации индивидуальных показате­лей эта мера более полезна, чем коэффи­циент надежности (r_t). Исходя из коэф­фициента надежности, стандартная О. и. определяется по формуле:

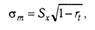
где S_x — стандартное отклонение резуль­татов теста в выборке, r_t — коэффициент надежности.

Стандартная О. и. и коэффициент на­дежности — взаимосвязанные способы выражения надежности. При этом О. и. не зависит от однородности выборки.

Важным аспектом применения крите­рия О. и. в психодиагностике являются анализ и интерпретация различий между результатами теста. Представление ре­зультатов в виде интервальных вероят­ностных значений предотвращает их ошибочное толкование как отражения ре­альной динамики измеряемого свойства у испытуемого, а также необоснованность констатации различий между средними показателями в сопоставляемых выбор­ках (см. Достоверность различий, Кри­терий χ²) при сравнении результатов не­скольких обследуемых или группы тесто­вых оценок у одного испытуемого. В пос­леднем случае при сопоставлении разных тестовых оценок, зная стандартные ошиб­ки показателей для одного и другого тес­та (или субтестов), стандартную ошибку различий ( _Δ) можно определить следую­щим образом:

или используя коэффициент надежности:

где S_x — стандартное отклонение, одина­ковое для двух тестов, поскольку перед сопоставлением оценок они переводятся в одну и ту же шкалу (см. Стандартиза­ция, Оценки шкальные).

Предположим, необходимо удостове­риться, существует ли у испытуемого раз­личие по оценкам вербальных и практи­ческих субтестов шкалы. Для Векслера интеллекта измерения шкалы r_t вер­бальных субтестов составляет 0,96, прак­тических — 0,93, значение стандартного отклонения для той и другой шкалы — 15. Тогда

Таким образом, для установления раз­личий между оценками с доверительной вероятностью примерно 68% необходимо, чтобы разность в оценках по названным шкалам не превышала 5 баллов. При дове­рительной вероятности Р = 0,05 значение σ_Δ удваивается, приближаясь к 10 баллам.

-П-

Дата добавления: 2015-07-10