Двухмодальные распределения

К ним относятся дискретное двузначное, арксинусоидальное и двухмодальные остро- и кругловершинные распределения.

Дискретное двузначное распределение — это распределение, при котором с равными вероятностями встречаются только два значения случайной величины. В центрированном виде (рис. 6.9) оно описывается формулой

где d(х) — дельта-функция Дирака; ±А — возможные значения случайной величины.

При дискретном двузначном распределении СКО равно значению параметра А, e = 1, к = 1, k = 0.

Рис. 6.9. Дискретное двузначное распределение

Дискретное двузначное распределение может быть приближенно предcтавлено в виде суммы двух нормальных распределений с одинаковыми по модулю, но противоположными по знаку МО и при стремлении r нулю их СКО:

Арксинусоидальное распределение (рис. 6.10) описывается выражением:

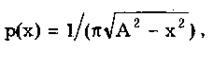
где А — параметр распределения. Его СКО равно , e = 1,5, к = 0,816, k = 1,11.

Рис. 6.10. Арксинусоидальное распределение при А = 1

Остро- и кругловершинные двухмодальные распределения получаются как композиция дискретного двузначного и экспоненциального распределений с различными значениями коэффициента а (рис. 6.11). При a < 2 получаются островершинные, при a > 2 — кругловершинные распределения.

Рис. 6.11. Островершинные (а) и кругловершинные (б)

двухнедельные распределения

Основными параметрами таких распределений являются:

• показатель относительного содержания в композиции дискретной составляющей С_д= s_д /s_экс= А/s_экс, где s_д и s_экс — СКО дискретного и экспоненциального распределений. Как правило, С_д Î (0;2).

Чем больше показатель С_д, тем больше провал. При С_д = 0 провал на графике распределения отсутствует;

• показатель степени a для экспоненциальных распределений, который обычно лежит в пределах от 0,5 до 2.

Островершинные распределения получаются при использовании некоторых высокоточных цифровых вольтметров, а кругловершинные распределения имеют погрешности от механического гистерезиса элементов приборов и датчиков.

Дата добавления: 2015-07-10