Столбцов матрицы

Алгоритмы обработки отдельной строки или столбца матрицы почти не отличаются от алгоритмов обработки элементов одномерного массива.

Например, найдем сумму элементов в первой строке матрицы А. Для этого зададим начальное значение суммы S=0, и организуем цикл для перебора элементов первой строки. Нужно помнить, что каждая строка матрицы содержит столько же элементов, сколько в этой матрице столбцов (смотри алгоритм на рис.30).

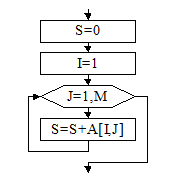
S:=0;

I:=1;

For J:=1 to M do

S:=S+A[i,j];

Рис.30

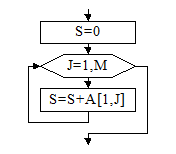Этот же алгоритм можно было записать следующим образом (рис.31):

S:=0;

For J:=1 to M do

S:=S+A[1,j];

Рис.31

Теперь найдем произведение четных элементов в последнем столбце матрицы. Для этого зададим начальное значение произведения P=1, и организуем цикл для перебора элементов последнего столбца. Каждый столбец матрицы содержит столько же элементов, сколько в этой матрице строк (алгоритм представлен на рис.32).

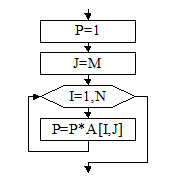
P:=1;

J:=M;

For I:=1 to N do

P:=P*A[i,j];

Рис.32

Этот же алгоритм можно было записать следующим образом (рис.33):

P:=1;

For I:=1 to N do

P:=P*A[i,M];

Рис.33

Дата добавления: 2015-07-10