Читайте также:
|
На рис. 47 приведена схема расположения элементов относительно главной диагонали.
Главная диагональ (ГД) Элементы, расположенные над ГД
| гд | |||
| Гд | ||
| ГД | |||
| гд |
Элементы, расположенные под ГД
Рис. 47
Рассмотрим элементы, расположенные над главной диагональю матрицы. Для матрицы А размером 4х4 эти элементы будут иметь следующие индексы:
в первой строке: A[1,2], A[1,3], A[1,4];
во второй строке: A[2,3], A[2,4];
в третьей строке: A[3,4];
в четвертой строке элементов нет.
Проанализировав полученные индексы, можно определить, что для элементов, расположенных выше главной диагонали, номер столбца всегда больше номера строки. Поэтому при организации циклов для обработки этих элементов нужно учитывать, что в первой строке нужно рассматривать элементы, начиная со второго столбца, во второй строке – начиная с третьего столбца, в третьей строке – начиная с четвертого столбца. В общем случае элементы i-ой строки нужно обрабатывать, начиная с элемента из i+1 столбца и заканчивая элементом последнего (N-го) столбца.
Для примера рассмотрим алгоритм нахождения суммы положительных элементов, расположенных над главной диагональю (рис. 48).
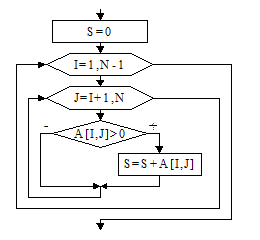
S:=0;
For i:=1 to N-1 do
For j:= I +1 to N do
If A[I,j]>0 then
S:=S+A[I,j];
Рис. 48
Рассмотрим элементы, расположенные под главной диагональю матрицы. Для матрицы А размером 4х4 эти элементы будут иметь следующие индексы:
в первой строке элементов нет;
во второй строке: A[2,1],
в третьей строке: A[3,1], А[3,2];
в четвертой строке: A[4,1], A[4,2], A[4,3].
Проанализировав полученные индексы, можно определить, что для элементов, расположенных ниже главной диагонали, номер столбца всегда меньше номера строки. Поэтому при организации циклов для обработки этих элементов нужно учитывать, что во второй строке нужно рассматривать элементы строки, заканчивая элементами из первого столбца, в третьей строке – заканчивая элементами из второго столбца, в четвертой строке – заканчивая элементами из третьего столбца. В общем случае элементы i-ой строки нужно обрабатывать, начиная с элемента из первого столбца и заканчивая рассмотрение элементами из i-1 столбца.
Для примера рассмотрим алгоритм нахождения произведения отрицательных элементов, расположенных под главной диагональю (рис. 49).
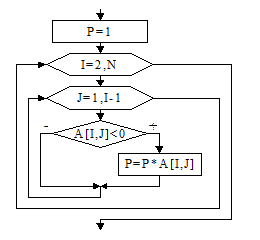
P:=1;
For i:=2 to N do
For j:= 1 to I-1 do
If A[I,j]<0 then
P:=P+A[I,j];
Рис. 49
На рис. 50 приведена схема расположения элементов относительно побочной диагонали.
Элементы, Побочная диагональ(ПД)
расположенные над ПД
| пд | |||
| Пд | ||
| Пд | |||
 пд
|
Элементы, расположенные под ПД
Рис. 50
Рассмотрим элементы, расположенные над побочной диагональю матрицы. Для матрицы А размером 4х4 эти элементы будут иметь следующие индексы:
в первой строке: A[1,1], A[1,2], A[1,3];
во второй строке: A[2,1], A[2,2];
в третьей строке: A[3,1];
в четвертой строке элементов нет.
В общем случае элементы i-ой строки нужно обрабатывать, начиная с элемента первого столбца и заканчивая элементом из N-i столбца.
Для примера рассмотрим алгоритм нахождения количества нулевых элементов, расположенных над побочной диагональю (рис. 51).
K:=0;
For i:=1 to N-1 do
For j:= 1 to N-i do
If A[I,j]=0 then
K:=K+1;
Рис.51
Теперь рассмотрим элементы, расположенные под побочной диагональю матрицы. Для матрицы А размером 4х4 эти элементы будут иметь следующие индексы:
в первой строке элементов нет;
во второй строке: A[2,4],
в третьей строке: A[3,3], А[3,4];
в четвертой строке: A[4,2], A[4,3], A[4,4].
В общем случае элементы i-ой строки нужно обрабатывать, начиная с элемента из столбца под номером N+2-I и заканчивая элементом из последнего (N-го столбца).
Для примера рассмотрим алгоритм нахождения максимального среди элементов, расположенных под побочной диагональю (рис. 52).
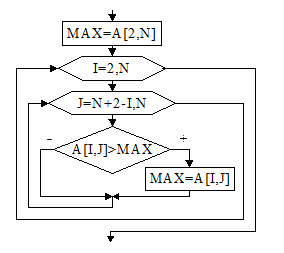MAX:=A[2,N]; {за начальное значения максимума берем любой элемент, расположенный под побочной диагональю}
For i:=2 to N do
For j:= N+2-i to N do
If A[I,j]>MAX then
MAX:=A[I,j];
Рис. 52
Дата добавления: 2015-07-10; просмотров: 222 | Нарушение авторских прав