Дискриминативность теста.

В параграфе 2 темы 1, посвященной содержанию и предмету психодиагностики, было отмече­но, что к психологическим измерениям предъявляются определенные научные требования. С точки зрения психометрики имеются пять характеристик, которым должны удовлетворять все методики и тесты для психологических измерений, к ним относятся: надеж­ность, дискриминативность, валидность, достоверность и репрезентативность.

Прежде чем переходить к обсуждению методов достижения валидности, рассмотрим способы установления дискриминативности. Под дискриминативностью теста будем понимать способность теста дифференциро­вать испытуемых в диапазоне от "макси­мального" до "минимального" результа­та набранного по данному теста.

Как отмечает П. Клайн [8], потенциально тест может быть гораздо более дискриминативным, чем другие средства измерения, например, интервью или рейтинги.

Показатели дискриминативности связаны по существу с ранжированием испытуемых. Основной пока­затель коэффициента дискриминативности, " õ" Фергюсона, который рекомендуется для оценивания дискриминатив­ности тестов, достаточно прост в вычислении. Если не касаться процедуры вывода формулы, то ее можно представить в следующем виде:

;

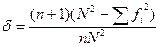где N - количество испытуемых, п - количество заданий,

f_{i -} частота встречаемости каждого показателя.

Коэффициент Фергюсона õ =0, когда все испытуемые получили одинаковые показатели, (то есть, когда нет дискриминативности), и равно 1 при равномерном (прямоугольном) распределении.

Вычислить õ Фергюсона можно следующим образом.

1. Подсчитать, как часто встречаются значения показателей для данного теста.

2. Возвести эти числа в квадрат и просуммировать: ;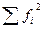

3. Прибавьте 1 к количеству заданий: п + 1.

4. Возвести в квадрат количество испытуемых: .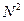

5. Перемножить количество заданий на результат шага (4): n .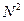

6. Подста­вить все найденные элементы в формулу.

Разработчик тестов должен учитывать некоторые характеристики õ коэффициента. Поскольку для равномерного (прямоугольного) распределения (наиболее дискриминативного) необходимы задания, в которых бы наиболее полно были реализованы все возможные проявления измеряемого свойства, это означает, что дискриминативность до некоторой степени проти­востоит надежности, так как использование заданий с широким пе­речнем возможных проявлений измеряемого свойства уменьшает взаимную корреляцию между заданиями (см. параграф 6).

Конечно, распределение показателей, которое дает тест – это, прежде всего, фун­кция трудности заданий, а это влияет не только на надежность, но также и на дискриминативность. Это означает, что при конст­руировании теста следует исходить из предназначения теста, поскольку именно этот факт определяет то, на что ориентироваться разработчику - на достижение максимальной надежности или максимальной дискримина­тивности.

Поскольку дискриминативность целого теста зависит от дискриминативности входящих в него заданий, рассмотрим проблему определения дискриминативности отдельных заданий теста.

Аналогично с определением дискриминативности целого теста под дискриминативностью отдельных пунктов будем понимать способность отдельных пунктов (заданий) теста дифференциро­вать обследуемых относительно "макси­мального" или "минимального" результа­та теста [3].

Любой ответ испытуемого на конкрет­ное задание можно оценить по двухбалль­ной шкале – "верно" (1 балл), "неверно" (0 баллов). Сумма баллов по всем пунк­там представляет собой первичную ("сы­рую") оценку. Мера соответствия успеш­ности выполнения одной задачи (одного пункта) всему те­сту является показателем дискриминативности задания теста для дан­ной выборки испытуемых и называется коэффициентом дискриминации (индек­сом дискриминации).

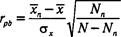
где x - среднее арифметическое всех индивидуальных оценок по тесту;

x _п - среднее арифметическое оценок по тес­ту у испытуемых, правильно выполнив­ших задание (в случае опросника личностности - соответствие с "клю­чом");

σ -среднеквадратическое от­клонение индивидуальных оценок по те­сту для выборки;

N_n- число испытуе­мых, правильно решивших задачу (или тех, чей ответ на данный пункт опросни­ка соответствует "ключу");

N - общее число испытуемых.

Коэффициент дискриминации может принимать значения от -1 до +1. Высокий положительный r свидетельствует об эффективности деления испытуемых. Вы­сокое отрицательное значение r свиде­тельствует о непригодности данного пункта для теста, о его несоответствии суммар­ному результату.

Индекс дискриминативности задания теста может быть вычислен с помощью метода контрастных групп. Необходимым условием приме­нения метода в этом случае является на­личие близкого к нормальному распреде­лению оценок по критерию валидизации. При этом, доля членов контрастных групп мо­жет изменяться в широких пределах в за­висимости от величины выборки. Чем больше выборка, тем меньшей долей ис­пытуемых можно ограничиться при выде­лении групп с высоким и низким резуль­татами. Чаще из выборки "извлека­ют" по 27% или 33% испытуемых.

Индекс дискриминации вычисляется с использованием формулы четырехпольного коэффициента корреляции:

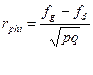где:

f_g - число лиц, правильно решивших задачу, по отношению к общему числу об­следованных в группе с максимальным ре­зультатом;

f_d - число лиц, правильно ре­шивших задание в группе с минимальным результатом;

р - общая пропорция пра­вильно выполненных заданий ;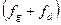

q — число лиц, давших неверное решение (1 - р).

Критические значения этого коэффи­циента, свидетельствующие о диагности­ческой ценности (на уровне р < 0,05), в зависимости от числа обследованных (п) приведены ниже:

n 25 50 100 200

r 0,39 0,28 0,20 0,14

Максимальная точность определения r достигается тогда, когда макси­мальная и минимальная группы составля­ют по 27% выборки.

При анализе дискриминативности задания теста особое внимание следует уделить определению статис­тической значимости коэффициентов корреляции. В тех случаях, когда значе­ние коэффициента дискриминации при­ближается к нулю и уровень значимостиневысок, проверяемый пункт теста дол­жен быть пересмотрен в связи с некоррек­тностью формулировки задания или вари­антов ответа на него [3].

Дата добавления: 2015-07-10