Метод вырезания узлов

Начинаем расчёт с узла А, где сходятся два стержня.

Следует изобразить тот узел, равновесие которого рассматривается (рис.21). Так как мы предполагаем, что все стержни растянуты, реакции стержней направляем от узла (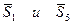). Тогда усилия в стержнях (реакции шарнира) будут направлены в противоположную сторону.

Для узла А составляем два уравнения равновесия:

∑ Х = 0:+Х_А + S₅ + S₁ ∙ cos 45° = 0;

∑ Y = 0:Y_А + S₁ ∙ cos 45° = 0.

Получаем: S₁ = -13.2 kH

S₅ = 29.32 kH

	Рис.21

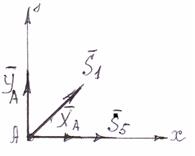
Далее рассматриваем равновесие узла С (рис.22).

Уравнения равновесия:

∑ Х = 0:Q + S₂ + S₆ ∙ cos 45° - S₁ ∙ cos 45°= 0;

∑ Y = 0:- S₁ ∙ cos 45° -

S₆ ∙ cos 45° = 0.

При подстановке значения S₁ учитываем, что усилие отрицательное.

Получаем: S₆ = 13.2 kH

S₂ = -48.7 kH

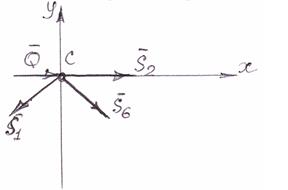
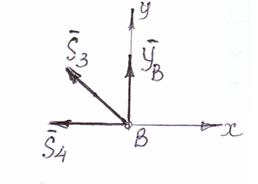
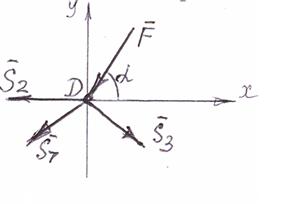
Аналогично рассчитываются остальные узлы (рис. 23,24).

∑ Х = 0:- S₂ – S₇ ∙ cos 45° - S₃ ∙ cos 45° - F ∙ cos α= 0;

Рис.22

∑Y=0:-S₇∙cos45°-S₃ ∙ cos 45° - F ∙ sin α = 0.

		Рис.24
	Рис.23

Рис.23

Отсюда: S₃ = -39.6 kH

S₇ = 15.13 kH

∑ Х = 0:- S₄ – S₃ ∙ cos 45° = 0;

Второе уравнение проверочное:

∑ Y = +Y_B + S₃ ∙ cos 45° = 28-39.6 ∙ 0.71 =0.

S₄ = 28.0 kH.

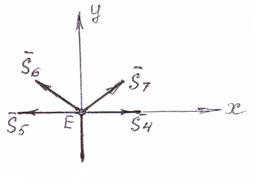
Для проверки рассмотрим равновесие узла Е (рис.25).

∑ Х = - S₅ + S₄ – S₆ ∙ cos 45° + S₇ ∙ cos 45° = 0;

Рис.25

∑ Y = S₆ ∙ cos 45° +

S₇ ∙ cos 45° - P = 0.

Так как уравнения обратились в тождества, то расчёт сделан верно.

Дата добавления: 2015-07-10