Равновесие конструкции

Задачи статики могут сводиться к рассмотрению равновесия конструкции, состоящей из системы тел, соединенных какими-либо связями (как правило, используется шарнирное закрепление, либо опирание одного тела на другое). Связи, соединяющие части данной конструкции, называют внутренними в отличие от внешних связей, скрепляющих конструкцию.

На рис. 11 представлена конструкция, которая состоит из двух тел (треугольников), скрепленных между собой шарниром С (внутренняя связь) и закреплена в точках А и В (внешние связи). Если мысленно отбросить неподвижные шарнирные опоры А и В (внешние связи), то конструкция не будет жесткой, поскольку треугольники могут поворачиваться вокруг шарнира С.

Система сил, действующих на такую конструкцию, должна при равновесии удовлетворять условиям равновесия твердого тела. Но эти условия, являясь необходимыми, не будут являться достаточными. Из них нельзя определить все неизвестные величины, и для решения задачи необходимо дополнительно рассмотреть равновесие какой-нибудь одной или нескольких частей конструкции.

Рис.11

Например, составляя условия равновесия для сил, действующих на всю данную конструкцию (на рисунке активные силы, действующие на нее, не показаны), получаем три уравнения равновесия с четырьмя неизвестными X_A,Y_A,X_B,Y_B. Рассмотрев дополнительно условия равновесия левого (или правого) треугольника, получаем еще три уравнения, содержащие два новых неизвестных X_C,Y_C - проекции реакции шарнира С (на рисунке не показаны). Решая полученную систему шести уравнений, можно найти все шесть неизвестных.

Другой способ решения подобных задач состоит в том, что конструкцию сразу разделяют на отдельные твердые тела и составляют уравнения равновесия каждого из тел в отдельности. При этом реакции внутренних связей будут попарно равны по модулю и противоположны по направлению. Для конструкции из N тел, на каждое из которых действует произвольная плоская система сил, получится таким образом 3N уравнений, позволяющих найти 3N неизвестных (при других системах сил число уравнений соответственно изменится).

Если для конструкции число всех реакций внешних и внутренних связей будет больше числа уравнений, в которые эти реакции входят, то конструкция будет статически неопределимой.

Пример 1 (определение реакций опор балки) Балка АВ концом А заделана в стену (рис.12), нагружена силой F = 20кН, равномерно распределенной нагрузкой постоянной интенсивности q = 3кН/м и парой сил с моментом М = 5кН・м.

Пренебрегая весом балки, определить реакции опоры А (жесткой заделки).

Для решения задачи воспользуемся общей схемой, изложенной в п.4.

1. Согласно схеме решения задач статики, определяем, что для нахождения неизвестных реакций необходимо рассмотреть равновесие балки.

В

Рис.12

1. На балку наложена связь в точке А типа жесткая заделка, поэтому освобождаем балку, заменив действие связи реакциями (x_A,y_A,M_A) (рис.13).

Непрерывно распределенную нагрузку q заменяем единой сосредоточенной силой Q, которая приложена посредине участка нагружения и имеет направление нагрузки q, величина силы Q=3q=9 кН.

В

Рис.13

1. В результате имеем равновесие свободной балки под действием плоской системы сил, в которой неизвестными являются реакции x_A,y_A,M_A
2. Выберем систему координат, как указано на рис.13. Составим уравнения равновесия:

1. Решаем полученную систему уравнений, находим неизвестные: x_A=10 кН, y_A=26,3 кН, M_A=98 кН∙м
2. Сделаем проверку, составив дополнительное моментное уравнение относительно свободного конца балки В:

Подставим в полученное уравнение найденные в п. 5 значения:

, в результате получаем , это означает, что задача решена верно!

Пример 2. Определить реакции шарнирных опор А и В балки, находящейся под действием сосредоточенной силы F = 60 Н, равномерно распределенной нагрузки с интенсивностью q = 15 Н/м и пары сил с моментом М = 40 Н · м; расстояние а = 1 м (рис.14).

Рис.14

Решение. Введем систему координат Oxy, совместив начало координат О с неподвижным шарниром А и направив ось Ox вдоль балки.

Для определения опорных реакций рассмотрим равновесие балки. К ней приложены активные силы: F, пара сил с моментом М и равномерно распределенная нагрузка. Заменим распределенную нагрузку ее равнодействующей Q, равной по модулю Q = q · 2a = 30 Н и приложенной в средней точке участка ее действия.

На балку наложены две связи: неподвижная шарнирная опора в точке А и подвижная шарнирная опора (каток) в точке В. Отбросим мысленно эти связи, заменив их соответствующими реакциями (рис.15).

Рис.15

Реакция R _A неизвестна по величине и направлению, поэтому разложим ее на две неизвестные по величине составляющие X _A, Y _A, направленные по координатным осям. Опора в точке В не препятствует ее перемещению вдоль наклонной плоскости и, следовательно, реакцию R _B следует направить перпендикулярно наклонной плоскости, то есть эта реакция известна по направлению, но неизвестна по величине.

Таким образом, в задаче имеется три неизвестных скалярных величины: X_A, Y_A, R_B. Поскольку для произвольной плоской системы сил имеется три независимых уравнения равновесия, данная задача является статически определимой.

Составим уравнения равновесия балки под действием плоской системы сил, содержащей заданные активные силы и неизвестные реакции связей, в форме (II):

F_ix = 0; M_А(F _i) = 0; M_В(F _i) = 0.

Эти уравнения равновесия записываются в рассматриваемом примере следующим образом:

система уравнений равновесия

F_ix = X_A - R_B sin 30° = 0;

M_А(F _i) = - Q · a + F · 2a + M + (R_B cos 30°) · 3a = 0;

M_В(F _i) = -Y_A · 3a + Q · 2a - F · a + M = 0.

Эта форма уравнений в данном случае обладает тем преимуществом, что каждое из двух уравнений моментов не содержит реакций, приложенных соответственно к моментным точкам А и В (так как их плечи относительно этих точек равны нулю).

Напомним, что алгебраические моменты сил берутся со знаком плюс, если они направлены против хода часовой стрелки. При вычислении момента реакции R _B относительно точки А выделена ее вертикальная составляющая, равная R_B cos 30° и имеющая плечо 3a, а горизонтальная составляющая имеет нулевой момент относительно точки А.

Из третьего и второго уравнений системы

R_B = (Q - 2F - M/a)/(3cos 30°) -50.0 Н;

Y_A = (2Q - F + M/a)/3 13.3 Н.

Полученное отрицательное значение R_B означает, что сила R _B направлена противоположно тому направлению, которое показано на рис.15

Для проверки можно составить уравнение проекций сил на ось Oy, которое должно удовлетворяться при найденных значениях Y_A и R_B:

F_iy = Y_A - Q + F + R_B cos 30° = 13.3 - 30 + 60 - 43.3 = 0.

Из первого уравнения системы находим

X_A = R_A sin 30° -25 Н.

Знак минус означает, что составляющая X _A в действительности направлена в отрицательном направлении оси Ox.

Модуль реакции R_A = (X_A² + Y_A²) 28.3 Н.

Пример 3 (определение реакций конструкции). Однородный стержень CD весом 346 H опирается на вертикаль­ную стойку AB. Определить реакции шарнирной опоры D, заделки A и силу взаимодействия балок AB и CD, если размеры BD=2м, BC=1м, AB=2м.

Решение. Система твердых тел состоит из двух балок (рис. 16). Рассмот­рим равновесие каждой из балок отдельно.

Рис.16 Рис.17

Отбрасываем связи, заменяя их дей­ствие реакциями (рис.17). На балку CDдействуют силы: G - вес балки ( задаваемая сила), X_D,Y_D - составляющие реакции шарнира D; N_B - реакция балки AB. На балку AB действуют силы: X_A, Y_A, m_A и N`<sub>B</sub> (реакция балки CD). По аксиоме о действии и противодействии: |N<sub>B</sub>|=-|N`_B|. Выбираем оси координат с началом в точке A.

Составим уравнения равновесия.

Для балки CD:

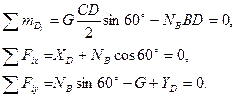
Для балки AB:

Из полученной системы находим

В качестве проверочного уравнения можно составить моментное уравнение, рассматривая конструкцию как одно твердое тело без учета внутренних связей.

6. Приложение методов статики к расчету фермы

При постройке мостов, подъемных кранов и других сооружений применяются конструкции, называемые фермами.

Фермой называется конструкция, состоящая из стержней, соединённых между собой на концах шарнирами и образующих геометрически неизменяемую систему.

Шарнирные соединения стержней фермы называют её узлами. Если оси всех стержней фермы лежат в одной плоскости, то ферма называется плоской.

Мы будем рассматривать только плоские фермы.

Предполагаем, что выполняются следующие условия:

1) все стержни фермы прямолинейные;

2) трение в шарнирах отсутствует;

3) все заданные силы приложены только в узлах фермы;

4) весом стержней можно пренебречь.

В этом случае каждый стержень фермы находится под действием только двух сил, которые будут вызывать его растяжение или сжатие.

Пусть ферма имеет m стержней и n узлов. Найдём зависимость между m и n, обеспечивающую жесткость конструкции (рис. 18).

Чтобы связать первые три узла, необходимо три стержня, для жесткого присоединения каждого из остальных (n-3) узлов нужно по 2 стержня, то есть

m - 3 = 2-(n-3)

или m = 2n-3. (1)

Если m < 2n - 3, то конструкция не будет геометрически неизменяемой, если m > 2n - 3, ферма будет иметь «лишний» стержень.

Равенство (1) называется условием жесткости.

Ферма, изображенная на рис. 18, является жесткой конструкцией

Рис.18

n=8, m= 13, 13=8 ∙ 2-3

Расчёт фермы сводится к определению опорных реакций и усилий в стержнях, то есть сил, действующих со стороны узлов на примыкающие к нему стержни.

Выясним, при каком соотношении между числом стержней и узлов ферма будет статически определимой. Если все неизвестные силы можно определить из уравнений равновесия, то есть количество независимых уравнений равно числу неизвестных, то конструкция статически определима.

Так как на каждый узел фермы действует плоская система сходящихся сил, то всегда можно составить 2n уравнений равновесия. Общее количество неизвестных - m + 3, (где m усилий в стержнях и 3 опорные реакции).

Условие статической определимости фермы

m + 3 = 2n

или m = 2n - 3 (2)

Сравнивая (2) с (1), видим, что условие статической определимости совпадает с условием жесткости. Следовательно, жёсткая ферма без лишних стержней является статически определимой.

---

Дата добавления: 2015-07-10