Вероятностная модель

Недостатком частотных методов взвешивания терминов является тот факт, что частотные веса рассчитываются формально, без учета реальных информационных потребностей. Для того чтобы установить соответствие между истинной информационной потребностью и терминами, составляющими поисковый образ документа, разработана вероятностная модель оценки весов терминов [1, 18].

Вероятностная модель основана на точной оценке вероятности того, что данный документ является релевантным (точнее, пертинентным) данному запросу [4, 34].

Обозначим вероятность такого события как , где – событие, которое состоит в том, что документ является релевантным по отношению к запросу . Аналогично, предположим, что – вероятность того, что документ окажется нерелевантным.

Для определения вероятности воспользуемся теоремой Байеса:

.

Здесь – вероятность того, что случайно выбранный документ является релевантным, – вероятность того, что из всего множества документов для рассмотрения выбран документ , – вероятность того, что документ выбран из множества релевантных документов.

Для дальнейшего изложения примем несколько упрощений. Во-первых, предположим, что поисковый образ документа представлен двоичным вектором (2.1):

,

где – размер словаря поисковой системы.

Далее, будем считать, что любая пара терминов входит в документ независимо друг от друга, то есть вероятности появления всех терминов в документе равны:

.

Тогда вероятность для документа будет равна произведению соответствующих вероятностей для всех входящих в него терминов:

.

(2.5)

Если вероятность появления термина в релевантном документе обозначить как

,

)

то выражение (2.5) можно представить в виде

,

(2.6)

где

.

Аналогично, для нерелевантных документов

,

(2.7)

где 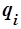– вероятность появления термина в нерелевантном документе, которая равна

В вероятностной модели считается, что адекватной мерой релевантности документа 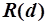является отношение

.

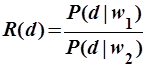Подставляя в это выражение формулы (2.6) и (2.7), получим

.

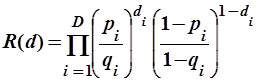(2.8)

После логарифмирования и упрощения выражения (2.8) меру релевантности можно описать следующим образом:

,

(2.9)

где

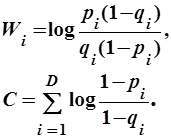
В выражении (2.9) есть вес термина в документе . В данном случае вес характеризует способность термина отличить релевантный документ от нерелевантного. Наименьший вес будут, очевидно, иметь общеупотребительные слова (термины из стоп-словаря), вероятности появления которых в релевантных и нерелевантных документах одинаковы и равны 50%.

Значение константы 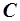одинаково для всех документов, поэтому обычно при вычислении релевантности ее игнорируют.

Для расчета вероятностей и часто используются упрощенные формулы

В этих формулах используются следующие обозначения:

– число документов информационного массива, в которых встречается термин ;

– число релевантных документов, в которых встречается этот термин;

– общее число релевантных документов;

– общее число документов в информационном массиве.

Таким образом, формула для определения веса термина примет вид

.

На практике в основном используется несколько измененное выражение [1, 34]:

.

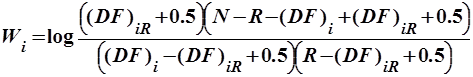(2.10)

Во время индексации величины и обычно неизвестны. Для их определения используется динамический итерационный процесс обратной связи с пользователем, который заключается в следующем.

При индексации величины и полагаются равными нулю, и вес термина рассчитывается как

.

При больших объемах информационного массива вес термина становится равным обратной документной частоте (2.4):

.

Когда информационно-поисковая система в ответ на запрос пользователя выдает список документов, пользователь может оценить релевантность некоторых из них. Если пользователь пометил несколько документов, которые являются пертинентными по отношению к его запросу, становится возможным определение значений и и, как следствие, более точный расчет весов терминов согласно выражению (2.10).

Процесс динамической подстройки весов терминов будет сходиться к некоторому оптимальному значению для каждого термина, поскольку ошибочно завышенные веса приведут к выдаче нерелевантных документов, в результате чего веса уменьшатся, в то время как ошибочно заниженные веса вызовут соответствующее увеличение веса терминов [1, 10, 18, 34].

Дата добавления: 2015-07-10