Косвенные измерения при нелинейной зависимости и некоррелированных погрешностях измерений аргументов

Для косвенных измерений при нелинейных зависимостях и некоррелированных погрешностях измерений аргументов используют метод линеаризации, предполагающий разложение нелинейной функции в ряд Тейлора:

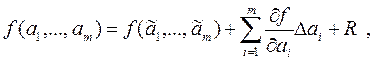
где f (a ₁,…, a_m) - нелинейная функциональная зависимость измеряемой величины от измеряемых аргументов a_i;

¶ f /¶ a_i, - первая производная от функции f по аргументу a_i, вычисленная в точках ;

- отклонение результата измерения аргумента a_i, от его среднего арифметического;

R - остаточный член. определенный по формуле:

Метод линеаризации допустим, если

Отклонения Δ a_i при этом должны быть взяты из полученных значений погрешностей и такими, чтобы они максимизировали выражение для остаточного члена R.

Результат измерения :

.

СКО случайной погрешности результата косвенного измерения

Доверительные границы случайной составляющей погрешности результата косвенного измерения ε(P) подставляя вместо коэффициентов b ₁ b ₂,..., b_m первые производные ¶ f /¶ a ₁, ¶ f /¶ a ₂,..., ¶ f /¶ a_m, соответственно.

НСП Θ(P) вычисляют, подставляя вместо коэффициентов b ₁, b ₂,..., b_m первые производные, ¶ f /¶ a ₁, ¶ f /¶ a ₂,..., ¶ f /¶ a_m, соответственно.

∆ (P) оценивают в соответствии с п. 2.

Дата добавления: 2015-07-10