Косвенные измерения при линейной зависимости аргументов

Искомое значение A связано с m измеряемыми аргументами

a ₁, a ₂,.., a_m уравнением

A = b ₁ a ₁ + b ₂ a ₂, +...+ b_m a_m,

где b ₁, b ₂,..., b_m - постоянные коэффициенты при аргументах a ₁, a ₂..., a_m соответственно.

Корреляция между ПИ аргументов отсутствует.

Если коэффициенты b ₁, b ₂,..., b_m определяют экспериментально, то сначала оценивают каждое слагаемое b_i · a_i; как косвенно измеряемую величину, полученную в результате произведения двух измеряемых величин, а потом находят оценку измеряемой величины A.

Результат косвенного измерения вычисляют по формуле

где - результат измерения аргумента а_i,

СКО результата косвенного измерения вычисляют по формуле

где - СКО результата измерения аргумента

Доверительные границы случайной составляющей погрешности результата косвенного измерения ε ( p ) вычисляют по формуле

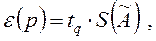
где t_q, - коэффициент Стьюдента, соответствующий доверительной вероятности P = l - q и числу степеней свободы f _эф, вычисляемому по формуле

где n_i, - число измерений при определении аргумента a_i.

Границы НСП A -Θ(p) вычисляют следующим образом.

Если НСП a_i заданы границами Θ _i, то Θ(p) при вероятности P вычисляют по формуле

где k - поправочный коэффициент, определяемый принятой доверительной вероятностью Р и числом m составляющих Θ _i.

При доверительной вероятности Р = 0,95 поправочный коэффициент k принимают равным 1,1.

При доверительной вероятности Р = 0,99 поправочный коэффициент принимают равным 1,4, если число суммируемых составляющих m >4. Если же число составляющих m ≤4, то поправочный коэффициент k ≤1,4; более точное значение k можно найти с помощью графика зависимости k = k (l,m), (рис.4).

Для нахождения k границы составляющих b_i Θ _i, располагают в порядке возрастания: b ₁Θ₁ ≤ b ₂Θ₂ ≤ b ₃Θ₃ ≤ b ₄Θ₄ и вычисляют отношения границ: l = b ₂Θ₂/ b ₁Θ₁, l ₂ = b_m Θ _m / b_{m- 1}Θ _{m- 1}. Затем по графику определяют значения k ₁ = k (l ₁, m) и k ₂ = k (l ₂, m); в качестве поправочного коэффициента принимают наибольшее из k ₁ и k ₂.

Если границы НСП a_i заданы доверительными интервалами с соответствующими вероятностям P_i, то границы Θ(p) для вероятности P вычисляют по формуле

Погрешность результата косвенного измерения ∆(P) оценивают на основе композиции распределений случайных и неисключенных систематических погрешностей.

Если , то за ∆(P) принимают Θ(p).

Если , то за ∆(P) принимают ε ( p ).

Если , то ∆(P) вычисляют по формуле

∆(P) = K (ε(P)+Θ(P)),

где K - коэффициент, зависящий от доверительной вероятности и от отношения .

Значения коэффициента K в зависимости от отношения для вероятности P = 0,95 и P = 0,99 приведено ниже:

Дата добавления: 2015-07-10