
Читайте также:
|
Если предполагают исследование и сопоставление результатов измерений или анализ погрешностей, то результат измерения и его погрешность представляют в виде

где n - число измерений того аргумента, при измерении которого выполнено минимальное число измерений.
Если границы погрешности результата измерения симметричны, то результат измерения и его погрешность представляют в виде

Пример 1. В этом примере определим погрешность измерения силы тока косвенным методом, посредством закона Ома.
Функциональная схема установки


|
Для начала найдем среднее арифметическое значение измеряемых величин
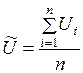 , , 
|
Среднеквадратическое отклонение измеряемых величин
 , , 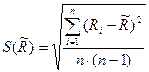
|
Зависимость измеряемой величины от аргументов нелинейна, поэтому для нахождения результата измерения и оценки его погрешностей следует воспользоваться методом линеаризации. Для данного типа задачи остаточный член находится по формуле:
 , ,
|
Где  ,
,  - максимальное отклонение результата измерения величины от ее среднего арифметического значения.
- максимальное отклонение результата измерения величины от ее среднего арифметического значения.
Знаки у слагаемых выражения берутся одинаковыми, т.к. погрешности  и
и  случайные.
случайные.
Сравниваем числовое значение  с числовым значением
с числовым значением  , где
, где

|
Если  , тогда
, тогда

|
Определим доверительные границы результата косвенного измерения
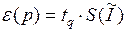
|
для этого определим коэффициент Стьюдента, который соответствует доверительной вероятности  и числу степеней свободы
и числу степеней свободы 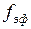
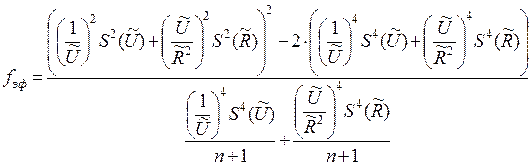
|
Определим систематическую погрешность результата косвенного измерения при условии, что заданы границы  и
и  .
.
 , ,
|
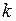 - определяем с помощью рисунка 4.
- определяем с помощью рисунка 4.
Определим систематическую погрешность результата косвенного измерения при условии, что границы неисключенных систематических погрешностей заданы доверительными границами, соответствующими вероятностям  и
и  .
.
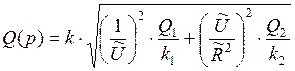 , ,
|
 ,
,  - согласно пункту 2.
- согласно пункту 2.
Запись результата измерения, представим в виде
 ,(А) ,(А)
|  ,(А) ,(А)
| 
| 
| 
| 
|
В данной задаче предполагалось равное количество измерений обоих параметров.
Пример 2. Определить погрешность измерения мощности косвенным методом с помощью вольтметра М3-22А, омметра М3 и потенциометра Р3003.Для большей наглядности будем использовать конкретные числовые значения, однократного измерения.
Функциональная схема.


|
Определим погрешность данного измерения
 , ,
|
где
 , ,  , ,  , ,
|
где
 ,
,  ,
,  - относительные погрешности каждой из величин соответственно.
- относительные погрешности каждой из величин соответственно.
Величины 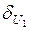 ,
,  ,
,  указаны в паспортах каждого из приборов соответственно.
указаны в паспортах каждого из приборов соответственно.
Пример 3. Определение коэффициента гармоник  и его погрешности косвенным методом с помощью вольтметра Ф5263 и анализатора С4-74 определяющего напряжение гармоник. При измерении первой гармоники использовали вольтметр Ф5263, второй и третьей анализатор гармоник С4-74 в режиме измерения напряжения.
и его погрешности косвенным методом с помощью вольтметра Ф5263 и анализатора С4-74 определяющего напряжение гармоник. При измерении первой гармоники использовали вольтметр Ф5263, второй и третьей анализатор гармоник С4-74 в режиме измерения напряжения.
Функциональная схема

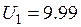 , В , В
|  . мВ . мВ
|  , мВ , мВ
|
Действительное значение коэффициента гармоник вычисляется по формуле
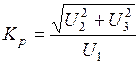 , ,
|
Где 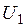 ,
,  ,
,  - напряжение 1,2,3 гармоник соответственно.
- напряжение 1,2,3 гармоник соответственно.

|
Определим погрешность измерения.

|
Для этого по паспортам данных приборов найдем их относительные и вычислим абсолютные погрешности.
| Ф5263 |  % %
| 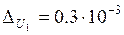
|
| С4-74 |  % %
| 
|
 % %
| 
|
Тогда, с учетом размерности

|
Получим значение абсолютной погрешности
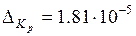
|
В конечном итоге получим
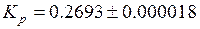
|
Пример 4. Необходимо определить ослабление аттенюатора и его погрешность, косвенным методом используя функциональную зависимость
 , ,
|
Где  ,
,  - напряжения, измеряемые вольтметром В2-38.
- напряжения, измеряемые вольтметром В2-38.
Функциональная схема

Измерив значения напряжений
 , В , В
| 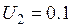 , В , В
|
Определим значение ослабления атеннюатора
 , Дб , Дб
|
Найдем погрешность измерения.

|
Для этого вычислим абсолютные погрешности измеряемых величин
| В2-38 |  % %
| 

|
Тогда с учетом того, что 

|
В конечном итоге получим

|
Дата добавления: 2015-07-10; просмотров: 58 | Нарушение авторских прав