Разветвленные электрические цепи. Правила Кирхгофа.

Изолированную замкнутую цепь мы уже рассматривали в предыдущем параграфе и результат представлен формулой (2.7'). С учетом того что полное сопротивление цепи R = R_e+R_i данное выражение преобразуется к виду

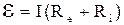, (4.1)

На рисунке 5 за положительный выбран обход по часовой стрелке где ε – сторонняя э.д.с. элемента, R_e и R_i – сопротивления внешней цепи и внутреннее сопротивление э.д.с. элемента. Если в изолированной замкнутой цепи имеется один источник сторонних э.д.с., то сила тока в цепи должна быть такой, чтобы суммарное падение напряжения на внешнем сопротивлении и внутреннем сопротивлении источника было равно сторонней э.д.с. источника. Если имеется несколько источников сторонних э.д.с, то надо взять их сумму со знаками, приняв в качестве положительной э.д.с. некоторого направления (принимаем за положительное направления обхода цепи либо обход по часовой стрелке либо против часовой). На рисунке 5 за положительный выбран обход по часовой стрелке. В каком направлении течет ток заранее неизвестно, поэтому за направление тока выбираем любое, например на рисунке 5 оно совпадает с положительным направлением обхода.

Знак э.д.с. берется положительным, если при движении по контуру в положительном направлении первым встречается отрицательный полюс источника. Если же первым встречается положительный полюс, то соответствующая э.д.с. будет с отрицательным знаком. Знак силы тока считается положительным, если направление тока совпадает с направлением обхода. В противном случае знак отрицательный. Таким образом, как э.д.с., так и сила тока являются алгебраическими величинами, принимающими как положительные, так и отрицательные значения. Теперь нетрудно обобщить уравнение (4.1) на произвольное число источников сторонних э.д.с. в изолированном замкнутом контуре: произведение алгебраического значения силы тока на сумму внешних и внутренних сопротивлений всех участков замкнутой цепи равно сумме алгебраических значений сторонних э.д.с. в замкнутом контуре:

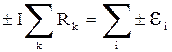, (4.1')

где ± перед I и ε_i означает, что знак должен быть выбран в соответствии с приведенными выше правилами.

Во многих практически важных случаях электрические цепи являются более сложными (разветвленными). Однако в цепь любой сложности входят элементы двух простейших видов:

1. узлов, в которых встречается более чем два проводника (рис. 6; точки C и D) – точки разветвления электрической цепи;

2. замкнутых контуров (рис. 6; контуры ABDCA, CDFEC, ABFEA).

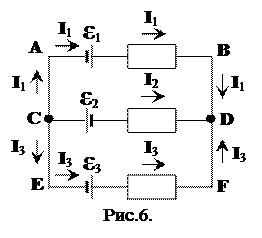Правила Кирхгофа служат для составления системы уравнений, из которой находятся силы тока для разветвленной цепи любой сложности. Они являются записью закона Ома (4.1') для каждого из замкнутых контуров и закона сохранения заряда в каждом узле. Правила знаков для сил тока и э.д.с. в каждом из замкнутых контуров таким же, как для изолированного контура. Направление положительного обхода для всех контуров выбирается одинаковым. Закон сохранения заряда в узлах требует, чтобы сумма сил токов, входящих в узел, была равна сумме сил токов выходящих из него, иначе говоря, сума алгебраических значений сил токов в узле должна быть равна 0. При составлении суммы силы токов, изображаемых стрелками с направлением от узла, берутся, например, со знаком минус, а силы токов, изображаемых стрелками с направлением к узлу, со знаком плюс. Можно брать обратные заки, это не изменит соответствующих уравнений, важно лишь для всех узлов применять одно и то же правило.

Таким образом, правила Кирхгофа гласят:

1. сумма произведений алгебраических значений сил токов на сопротивление соответствующих участков каждого из замкнутых контуров равна сумме алгебраических значений сторонних э.д.с. в каждом замкнутом контуре: 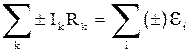; (4.2)

2. сумма алгебраических значений сил токов в каждом узле, равна нулю: 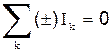(4.3)

Получающаяся система уравнений для любой разветвленной цепи является полной и позволяет определить все токи.

Дата добавления: 2015-07-10