|
Читайте также: |
§1. Электрический ток и его характеристики (сила и плотность тока)
║Электрическим током называется упорядоченное движение заряженных ║частиц или заряженных макроскопических тел.
Различают два вида электрических токов: токи проводимости и конвекционные токи.
║Электрическим током проводимости называется упорядоченное движение в ║веществе или в вакууме свободных заряженных частиц – носителей тока.
Например: электрические токи в металлах, электролитах, ионизированных газах, плазме, полупроводниках, пучки электронов или ионов в вакууме.
Носителями тока в металлах являются электроны проводимости, в электролитах – ионы, в газах и плазме– ионы и электроны, в полупроводниках – электроны проводимости и дырки.
║Конвекционным электрическим током (электрическим током переноса) ║называется электрический ток осуществляемый движением в пространстве ║заряженного макроскопического тела.
Например, движущаяся заряженная лента электростатического генератора, изготовленная из диэлектрического материала, образует конвекционный ток.
За направление электрического тока условно принимают направление движения положительных зарядов, образующих этот ток. Если движутся не положительные, а отрицательные заряды, то направление электрического тока считается противоположным направлению движения отрицательных зарядов.
Ток проводимости возникает под действием электрического поля. При этом равновесное (электростатическое) распределение зарядов в проводнике нарушается, а его поверхность и объем перестают быть эквипотенциальными. Внутри проводника появляется электрическое поле, а касательная составляющая напряженности электрического поля у поверхности проводника Еτ≠0. Электрический ток в проводнике продолжается до тех пор, пока все точки проводника не станут эквипотенциальными. Для существования в среде тока проводимости необходимо выполнение двух условий:
1. в среде должны быть носители тока,
2. в ней должно существовать электрическое поле.
Для поддержания ока необходим источник электрической энергии – устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического тока.
Линии вдоль которых движутся заряженные частицы, названы линиями тока. За направление линий тока принимают направление движения положительных зарядов. Прочерчивая линии тока мы получаем наглядное представление о движении электронов и ионов, образующем ток.
Если внутри проводника с током мысленно выделить трубку, у которой боковая поверхность состоит из линий тока, то заряженные частицы при движении не будут пересекать боковую поверхность трубки и не будут ни выходить из трубки наружу, ни входить извне в трубку. Такая трубка называется трубкой тока (рис.1.). Поверхность металлической проволоки, находящейся в изоляторе, есть одна из трубок тока.
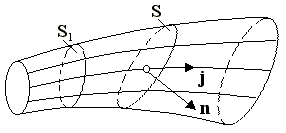
Рис. 1. Трубка тока.
Для количественной характеристики электрического тока служат две основные величины: плотность тока и сила тока
1. Для характеристики направления электрического тока в разных точках рассматриваемой поверхности и распределения силы тока по этой поверхности вводится вектор плотности тока.
║Плотностью электрического тока проводимости называется вектор j, ║совпадающий с направлением электрического тока в рассматриваемой точке ║и численно равный отношению силы тока dI сквозь малый элемент ║поверхности, ортогональной направлению тока, к площади dS┴ этого ║элемента:
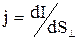. (1.1)
Плотность тока равна заряду, походящему в единицу времени через единицу поверхности.
Выдели м внутри проводника площадку с S=1, расположенную перпендикулярно к линиям тока, а значит, и перпендикулярно к направлению скорости v заряженных частиц (рис. 2.)
 |
Построим на этой площадке прямоугольный параллелепипед с длиной равной скорости движения частиц v. Тогда число частиц, которые пройдут через рассматриваемую площадку в единицу времени, будет равно числу частиц, заключенных внутри параллелепипеда. Если n концентрация заряженных частиц, то число частиц внутри параллелепипеда равно nv (т.к. S=1), а заряд переносимый ими, есть nve, где е – заряд одной частицы (например, электрона). Поэтому плотность тока j равна
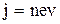. (1.2)
Т.к. n и е скалярные величины, а скорость – вектор, то можно ввести вектор плотности тока j, определяемый следующим образом
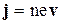(1.2')
Т.к. скорость v характеризует движение заряженных частиц в данной точке, то и вектор плотности тока j определяет электрический ток в данной точке.
Если выделить внутри проводника бесконечно малую площадку dS, перпендикулярную к вектору плотности тока j, то заряд, проходящий через нее за время dt, равен
,
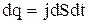Если площадка dS не перпендикулярна к j, то в этом выражении вместо j нужно взять составляющую плотности тока jn (проекция плотности тока на нормаль), перпендикулярную к dS.
2. Сила тока.
║Силой тока (или просто током) называется скалярная физическая величина ║ I, равная отношению заряда dq, переносимого при электрическом токе сквозь ║рассматриваемую поверхность S за малый промежуток времени, к ║длительности dt этого промежутка.
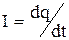. (1.3)
В случае тока проводимости в какой-либо электрической цепи под поверхностью S понимают поперечное сечение проводника.
Зная вектор плотности тока в каждой точке проводника, можно выразить через него и силу тока
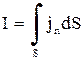, (1.4)
где интегрирование производится по всей поверхности S любого сечения проводника.
Если малый элемент поверхности площадью dS расположен так, что нормаль n к этому элементу составляет с вектором плотности тока угол α, то сила тока сквозь участок поверхности dS равна (см.уравнение1.1)
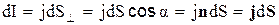
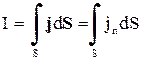. (1.4')
В однородном цилиндрическом проводнике ток равномерно распределяется по его сечению, так что
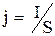(1.5)
Единицей силы тока служит ампер (А). Эта единица является одной из основных единиц системы СИ. При токе в 1А через полное сечение проводника протекает заряд 1Кл за время 1с. Единица плотности тока – ампер на квадратный метр (А/м2).
Если плотность тока и сила тока не меняются в проводнике во времени, то мы говорим, что в проводнике имеется постоянный, или стационарный ток
║Электрический ток называется постоянным, если его направление и сила ║тока не изменяются с течением времени.
Для постоянного тока выражение (1.3) преобразуется
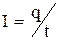, (1.3')
где q – заряд, переносимый сквозь рассматриваемую поверхность за конечный промежуток времени t.
Для постоянства электрического тока проводимости необходимо, чтобы напряженность электрического поля во всех точках проводника, по которому идет ток, сохранялась неизменной. Поэтому заряды не должны накапливаться или убывать где-либо в проводнике, по которому идет постоянный электрический ток. В противном случае изменялось бы электрическое поле этих зарядов. Это означает, что цепь постоянного тока должна быть замкнутой, а сила тока – одинаковой во всех направлениях.
Рассмотрим внутри проводника с током какую либо замкнутую поверхность S и будем понимать под jn проекцию вектора плотности тока j на внешнюю нормаль к элементу поверхности dS. Тогда из определения плотности тока следует, что положительный заряд, уходящий в единицу времени через всю поверхность S наружу, есть
,
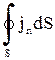где интегрирование проводится по всей замкнутой поверхности dS. Вместе с тем, согласно одному из основных законов электричества, электрические заряды сохраняются: они только перераспределяются между телами (или различными частями тел), но полная сумма возникающих положительных и отрицательных зарядов равна нулю. Поэтому, если dq/dt есть изменение за единицу времени положительного заряда, заключенного внутри замкнутой поверхности S, то
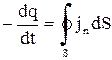. (1.6)
Пусть S – замкнута поверхность, а векторы d S всюду проведены по внешним нормалям n. Тогда поток вектора j сквозь эту поверхность S равен электрическому току I, идущему вовне из области, ограниченной замкнутой поверхностью S. Согласно приведенному выше закону сохранения электрического заряда суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время dt на dq = – Idt, т.е.
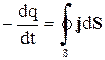. (1.6')
Эти соотношения 1.5 и 1.5' называются уравнением непрерывности.
В случае постоянного тока q=const и
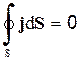(1.6")
Дата добавления: 2015-07-10; просмотров: 189 | Нарушение авторских прав