Закон Ома для участка цепи с источником ЭДС и для полной цепи

Закон Ома (основной закон постоянного тока), открытый экспериментально (является обобщений данных опытов), гласит:

║Сила тока, протекающего по однородному проводнику, пропорциональна ║разности потенциалов на его концах (напряжению U₁₂):

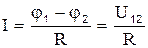, (2.1)

где R – электрическое сопротивление проводника, [R] – 1Ом.

Сопротивление R зависит от формы и размеров проводника, от его материала и температуры, а также от конфигурации (распределения) тока по проводнику. В общем случае объемного распределения тока нельзя говорить о сопротивлении, пока не указаны или расположение проводящих к интересующему нас проводника проводов, или конфигурация тока.

В простейшем случае однородного цилиндрического проводника сопротивление

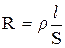, (2.2)

где l – длина проводника, S – площадь его поперечного сечения, ρ – удельное электрическое сопротивление характеризующее вещество проводника, [ ρ ] – Омּм..

Закон Ома (2.1) и формула (2.2.) позволяют найти силу тока в проволоках и вообще в тех случаях, когда трубки тока являются цилиндрами постоянного сечения. Однако часто приходится вычислять силу тока в проводящих средах, в которых, трубки тока не имеют цилиндрической формы. Примерами могут служить сферический и цилиндрический конденсаторы, в которых пространство между обкладками заполнено проводящей средой. В этом случае формула (2.1) неприменима, так как расстояние l различно для разных точек поверхности обкладок, а площадь S у каждой обкладки имеет разную величину.

Однако закон Ома можно представить в другой форме, которая пригодна и для решения задач о токах в проводящих средах.

Разность потенциалов в формуле (2.1) согласно определению потенциала электростатического поля, модно выразить через линейный интеграл напряженности поля Е, взятый от начального до конечного сечения рассматриваемого участка проводника

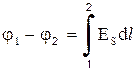, (2.3)

где d l – элемент длины проводника. Линейный интеграл напряженности электрического поля между точками 1 и 2 носит название напряжения, существующего между этими точками U₁₂. Внося 2.3 в 2.1, получаем:

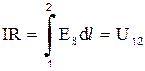. (2.4)

Эта формула закона Ома в случае постоянного электрического поля равносильна формуле (2.1). Однако она обладает тем преимуществом, что остается применимой и к переменным (квазистационарным) токам.

Воспользовавшись понятием плотности тока, мы можем выразить закон Ома в дифференциальной форме, устанавливающей связь между величинами, относящимися к одной определенной точке проводника, тогда как закон Ома в интегральной форме (2.1), (2.4) связывает величины, относящиеся к различным точкам (φ₁ и φ₂) или к конечным отрезкам (R) проводника.

Рассмотрим какой либо однородный по составу и цилиндрической по форме участок проводника. Если вместо удельного сопротивления ρ в уравнении (2.2) ввести обратную ему величину – удельную проводимость, или электропроводность λ=1/ ρ, то оно примет вид

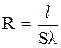. (2.5)

Внося это выражение в (2.4), получим:

,

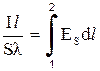или в виду (1.5)

.

В случае постоянного тока в однородном цилиндрическом проводнике, ввиду тождества физических условий по всей его длине слагающая поля по оси проводника Е_s, очевидно имеет постоянное значение, так что

,

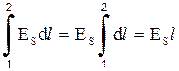и следовательно

.

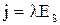В каждой точке проводника направление тока совпадает с направлением электрического поля, обуславливающего движение зарядов. Стало быть, вектор плотности тока должен совпадать по направлению с вектором Е, и последнее уравнение может быть записано окончательно в виде

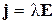. (2.6)

Это соотношение выражает закон Ома в дифференциальной форме. В (2.6) нет дифференциалов (производных), а свое название это выражение получило потому, что в нем устанавливается связь между величинами, относящимися к одной и той же точке проводника.

Допустим, что единственными источниками электрического поля Е в проводниках, по которым текут токи, являются электрические заряды, возбуждающие поля по закону Кулона. При прохождении тока непрерывно происходит убыль зарядов, точнее, нейтрализация положительного и отрицательного электричеств. Для того чтобы напряженность поля Е, а с ней и плотность электрического тока j оставались неизменными, необходимы какие-то дополнительные силы или процессы, непрерывно пополняющие электрические заряды. Плотность электрического тока определяется полной силой F, действующей на электрон или другой носитель зарядов. Силу F можно разложить на две части: силу электрическую и силу неэлектрическую, включающую в себя все прочие силы. Эти силы принято называть сторонними. С учетом сторонних сил закон Ома (2.6) записывается в виде

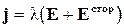, (2.6')

где Е ^стор – напряженность поля сторонних сил, т.е. сторонняя сила, отнесенная к единице заряда. Соотношение (2.6') выражает локальный закон Ома.

Рассмотрим важнейший случай, когда электрические токи текут вдоль тонких проводов. Направление тока будет совпадать с направлением оси провода. Это автоматически обеспечивается соответствующим распределением электрических зарядов на поверхностях проводников или в местах, где действуют сторонние силы. Площадь поперечного сечения провода S в различных местах его может быть неодинаковой. Для тонких проводов плотность тока j может считаться одной и той же во всех точках поперечного сечения. Через поперечное сечение провода в единицу времени проходит количество электричества

.

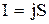Если ток постоянен, то из-за сохранения заряда величина I будет одна и та же вдоль всего провода. Для общности будем предполагать, что в проводнике действуют сторонние силы, например, имеется гальванический элемент. Воспользуемся законом Ома в форме (2.6'). Из него получаем

.

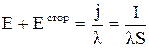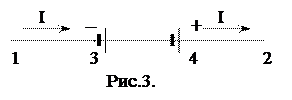Умножим это соотношение на элемент длины провода d l и проинтегрируем по участку провода от какой-либо точки 1 до другой точки 2 (рис. 3). Поскольку ток один и тот же во всем проводе, величину I можно вынести из-под знака интеграла. Сделав это, найдем .

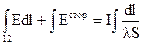Так как электрическое поле стационарных токов потенциально, то первый интеграл выражается через разность потенциалов φ₁–φ₂. Второй интеграл достаточно распространить на ту часть пути, где Е^стор ≠ 0, т.е. на ту часть которая проходит внутри гальванического элемента. Этот интеграл на зависит от положения начальной и конечной точек 1 и 2. Требуется только, чтобы эти точки находились вне гальванического элемента. Ввиду потенциального характера пола Е^стор в области, где действуют сторонние силы, интеграл не зависит также от того, как проходит путь интегрирования через гальванический элемент. Значит, этот интеграл есть величина характеризующая свойства самого элемента. Она называется электродвижущей силой элемента:

.

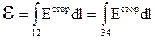Электродвижущая сила положительна, если путь 12 пересекает гальванический элемент в направлении от катода к аноду, и отрицательна в противоположном случае. Третий интеграл

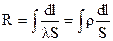
есть величина, характеризующая провод, по которому течет электрический ток – электрическое сопротивление провода. Если провод изготовлен из однородного материала и всюду имеет одинаковую толщину, то получается формула (2.2).

Таким образом,

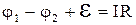. (2.7)

Формула (2.7) выражает закон Ома в интегральной форме. Ее называют законом Ома для участка цепи. R есть сопротивление всего участка, включая сопротивление самого элемента. Если участок не содержит гальванического элемента (или, вообще, на нем действуют сторонние силы), то формула (2.7) принимает вид (2.1).

Если начальная и конечная точки 1 и 2 совпадают, то φ₁ – φ₂ = 0 и формула (2.7) переходит в закон Ома для влей (замкнутой) цепи:

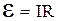. (2.7')

Здесь R означает уже полное сопротивление всей цепи. Если φ_а – потенциал анода, а φ_к – катода, то φ_а – φ_к = R_eI, где R_e – сопротивление всего внешнего участка цепи. Сравнивая это соотношение с (2.7') получим

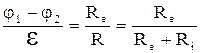, (2.8)

где R_i – внутреннее сопротивление самого элемента. Отсюда следует, что всегда, когда по цепи течет ток, разность потенциалов между полюсами элемента φ_а – φ_к меньше электродвижущей силы. Только в предельном случае, когда R_e → ∞ (а следовательно, I → 0), получается

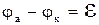. (2.8')

Значит, электродвижущую силу можно определить как разность потенциалов между полюсами разомкнутого источника тока.

§3. Закон Джоуля – Ленца в дифференциальной форме.

С прохождением тока неразрывно связано выделение тепла (нагревание проводников) в цепи тока.

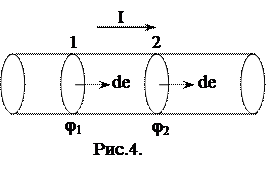Количества тепла Q, выделяемое током в единицу времени в каком-либо участке цепи, может быть определено следующим образом. Если силе тока в проводнике равна I, то за элемент времени dt через каждое сечение проводника протекает de = Idt единиц электричества; в частности, сколько единиц электричества протекает через начальное сечение 1 внутрь рассматриваемого участка проводника, такое же количество электричества выйдет из этого участка через сечение 2 (рис. 4). Так как распределение зарядов в проводнике остается при этом неизменным (постоянный ток), то весь процесс эквивалентен непосредственному переносу de единиц электричества от сечения 1 к сечению 2.

Совершаемая при этом переносе работа электрических сил равна:

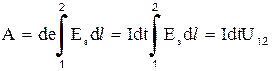, (3.1)

где линейный интеграл может быть взят по оси цилиндрического проводника. Согласно закону сохранения энергии, эквивалентное работе электрических сил количество энергии должно выделиться в виде иной формы энергии (например,

в форме тепла). Следовательно, выделяемая током энергия равна:

,

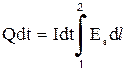откуда

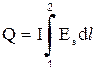. (3.2)

Воспользовавшись законом Ома в форме (2.4), получим:

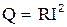. (3.3)

В том случае, если поле Е обладает потенциалом φ, как это имеет место для поля постоянных токов, мы можем, согласно (2.3) записать это уравнение так:

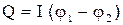. (3.4)

Если проводник неподвижен и если в нем не происходит химических реакций (электролиты), то это количество энергии Q выделяется током в форме тепла. Уравнения (3.3) и (3.4) выражают закон Джоуля – Ленца.

Величина Q равная количеству выделяющейся в единицу времени энергии имеет размерность мощности (1ватт = джоуль/сек) или выражается в тепловой мере (в калориях в секунду).

Закон Джоуля – Ленца (3.3) носящий характер закона интегрального, может быть, подобно закону Ома, преобразован в форму дифференциальную. С этой целью введем вместо Q удельную мощность тока 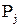, т.е. количество тепла, выделяющееся за секунду в единице объема проводника:

,

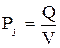где V – объем участка проводника, в котором выделяется общее количество тепла Q (Если выделение тепла происходит неравномерно по объему проводника, то значение 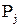в каждой точке проводника определяется соотношением ).

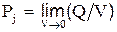Рассмотрим опять однородный цилиндрический проводник сечения S, длины l и объема V=S l. Согласно (3.3) и (2.5), получим:

,

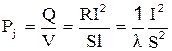откуда на основании (1.5)

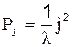, (3.5)

или на основании (2.6)

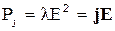. (3.6)

Оба эти выражения являются записью закона Джоуля – Ленца в дифференциальной форме. Уравнение (3.5) представляет собой наиболее общую формулировку данного закона, применимую к любым проводникам, вне зависимости от их формы, однородности и т.д., наконец, вне зависимости от того, имеем ли мы дело с постоянным или переменным током.

Дата добавления: 2015-07-10