Читайте также:
|
Интегральная форма вышеуказанных законов постоянного тока удобна для однородных проводников, имеющих постоянное сечение, однако часто проводящая среда имеет более сложную форму и неоднородную структуру. Для таких ситуаций получим иные формулировки тех же законов.
Для этого мысленно выделим внутри проводящей среды некоторый цилиндрический объем с площадью основания dS, образующие dl которого параллельны вектору плотности тока в этой области.
Сопротивление этой трубки тока  ,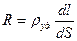
напряжение, приложенное к цилиндру U=Edl
и сила тока в нем I=jdS.
| (4.1) |
Подставим эти значения в закон Ома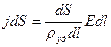 
. Носители заряда в каждой точке движутся в направлении вектора напряженности, поэтому направления 
и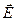 
совпадают. Тогда можем записать
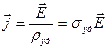, (4.2)
где σуд – удельная электропроводность. Выражение (4.2) является законом Ома в дифференциальной форме. Его можно применять для любых проводящих сред.
Если на участке цепи имеется источник питания с ЭДС, тогда
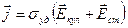. (4.3)
Таким образом, для возникновения электрического тока необходимы носители тока и электрическое поле напряженностью 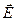, под действием которого заряды будут перемещаться.
С помощью формул (4.1) представим закон Джоуля-Ленца для элементарного цилиндра
.
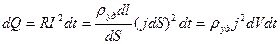Количество теплоты, выделяющееся в единице объема проводника за единицу времени, называется удельной тепловой мощностью:
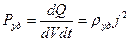или 
.
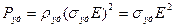(4.4)
Это закон Джоуля-Ленца в дифференциальной форме.
Если участок цепи неоднороден, то
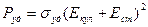. (4.5)
Чтобы получить количество теплоты, выделяющееся во всем проводнике за время t нужно проинтегрировать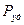 
по объему проводника в некоторый момент времени, а затем полученное выражение проинтегрировать по времени
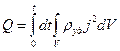. (4.6)
Дата добавления: 2015-07-10; просмотров: 100 | Нарушение авторских прав