Читайте также:
|
В персональном компьютере (ПК) применяются две формы представления чисел:
• естественная форма, или форма с фиксированной запятой (точкой) - ФЗ (ФТ);
• нормализованная (нормальная) форма, или форма с плавающей запятой (точкой) - ПЗ (ПТ).
В форме представления с ФЗ числа представляются в виде последовательности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной части. Например, если числа представлены в двоичной системе счисления и имеют пять разрядов в целой части числа (до запятой) и пять в дробной части (после запятой), то числа + 10111,1011(2) и - 1001,10101(2), записанные в такую разрядную сетку, будут иметь вид:
+ 10111,10110
- 01001,10101.
Эта форма проста, естественна, но имеет небольшой диапазон представления чисел и поэтому чаще всего неприемлема при вычислениях.
Диапазон значащих чисел N в системе счисления с основанием Р при наличии m разрядов в целой части и s разрядов в дробной части числа (без учёта знака числа) будет таким:
.
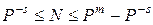Например, при Р = 2, m = 10 и s = 6 числа изменяются в диапазоне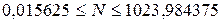 
. Если в результате операций над числами получится число, выходящее за допустимые пределы, произойдёт переполнение разрядной сетки, и дальнейшие вычисления теряют смысл.
В современных компьютерах естественная форма представления используется как вспомогательная и только для целых чисел.
В памяти ПК числа с ФЗ хранятся в трёх форматах: полуслово - это 16 бит (2 байта); слово - 32 бита (4 байта); двойное слово – 64 бита (8 байтов).
Отрицательные числа с ФЗ записываются в разрядную сетку в дополнительных кодах, которые образуются прибавлением единицы к младшему разряду обратного кода. Обратный код получается заменой единиц на нули, а нулей на единицы в прямом двоичном коде.
В форме представления с ПЗ число изображается в виде двух групп цифр:
• мантисса;
• порядок.
При этом абсолютная величина мантиссы должна быть меньше 1, а порядок должен быть целым числом. В общем виде число в форме с ПЗ может быть представлено так:
,
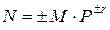где М - мантисса числа (| М | < 1), старший разряд которой является значащим (равным единице за исключением записи числа ноль);
Р - основание системы счисления;
r - порядок числа (целое число в системе счисления с основанием Р, равное количеству разрядов сдвига исходного числа (вправо – со знаком «+», влево – со знаком «-») при его записи в мантиссе).
Например, приведённые ранее числа в нормализованной форме запишутся следующим образом:
+ 0,101111011×2+101
- 0,1001010101×2+100.
Нормализованная форма представления обеспечивает большой диапазон отображения чисел и является основной в современных компьютерах. Так, диапазон значащих чисел в системе счисления с основанием Р при наличии m разрядов у мантиссы и s разрядов у порядка (без учёта знаковых разрядов порядка и мантиссы) будет:
.
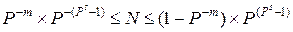Например, при Р = 2, m = 22 и s = 10 диапазон чисел простирается примерно от 10-300 до 10300. Для сравнения: количество секунд, которые прошли с момента образования планет Солнечной системы, составляет около 1018.
В памяти ПК числа с ПЗ хранятся в двух форматах: слово - 32 бита (4 байта); двойное слово - 64 бита (8 байт).
Разрядная сетка для чисел с ПЗ имеет следующую структуру (см. рис. 4.10). В двух старших разрядах записываются знак числа и знак порядка, соответственно (1 - «минус» или 0 - «плюс»). Далее в прямом двоичном коде записывается порядок числа (справа налево); пустые разряды слева заполняются нулями. В остальных разрядах указывается мантисса (слева направо); пустые разряды справа заполняются нулями.
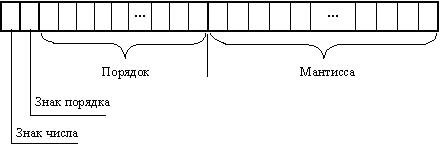
Рис. 4.10. Разрядная сетка для чисел с плавающей точкой
В качестве примера рассмотрим запись десятичного числа - 6,25(10) - в четырехбайтовом формате с семью разрядами для записи порядка (см. рис. 4.11). Так, в результате перевода числа 6,25(10) в двоичную систему счисления и его нормализации получим:
- 6,25(10) = - 110,01(2) = - 0,11001×2+11.
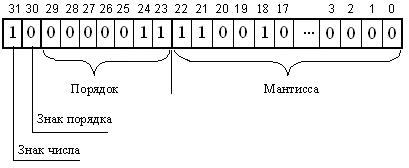
Рис. 4.11. Пример записи числа в нормализованном виде
Дата добавления: 2015-07-10; просмотров: 70 | Нарушение авторских прав