Измерение количества информации

Американский инженер Р. Хартли в 1928 г. предложил рассматривать процесс получения информации как выбор одного сообщения из конечного заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, как двоичный логарифм N:

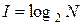или 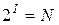, (4.1)

где N – количество равновероятных сообщений (число возможных выборов);

I – количество информации.

Если N = 2 (выбор из двух возможностей), то I = 1 бит.

Таким образом, бит [1]в теории информации - количество информации, необходимое для различения двух равновероятных сообщений («орёл-решка», «чёт-нечёт» и т. п.).

Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле (4.1) Хартли можно вычислить, какое количество информации для этого требуется:

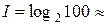6,644 бит,

т.е. сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации.

В вычислительной технике битом называют наименьшую «порцию» памяти компьютера, необходимую для хранения одного из двух знаков 0 и 1, используемых для машинного представления данных и команд.

Формула Хартли широко применяется при кодировании информации, поскольку позволяет рассчитать минимальную длину кода I (т.е. количество разрядов памяти, выделяемое для хранения информации в двоичном коде) в двоичном алфавите при известном количестве символов N, подлежащих кодированию.

Например, рассчитаем, сколько нужно разрядов памяти для хранения чисел в диапазоне от 0 до 17. Здесь количество символов, подлежащих кодированию 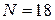, тогда используя формулу (4.1), имеем 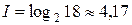, т.е. для хранения таких чисел необходимо 5 разрядов памяти или 5 бит.

Решим обратную задачу. Пусть известен объём памяти для хранения символов, например I = 12 бит, требуется найти количество символов N, которые можно закодировать в таком объёме в двоичном коде. Используя формулу Хартли 2 ^I = N, имеем 2¹² = 4096 символов.

За единицу информации можно было бы выбрать количество информации, необходимое для различения, например, десяти равновероятных сообщений. Тогда это уже будет не двоичная (бит), а десятичная (дит) единица информации.

Поскольку бит - слишком мелкая единица измерения, на практике чаще применяется более крупная единица - байт, равная восьми битам. В частности, восемь бит требуется для того, чтобы закодировать любой из 256 символов основного компьютерного кода ASCII (256 = 2⁸).

Используются также более крупные производные единицы информации:

Килобайт (Кбайт) = 1024 байт = 2¹⁰ байт;

Мегабайт (Мбайт) = 1024 Кбайт = 2²⁰ байт;

Гигабайт (Гбайт) = 1024 Мбайт = 2³⁰ байт.

В последнее время в связи с увеличением объёмов обрабатываемой информации входят в употребление такие производные единицы, как:

Терабайт (Тбайт) = 1024 Гбайт = 2⁴⁰ байт;

Петабайт (Пбайт) = 1024 Тбайт = 2⁵⁰ байт и пр.

4.4.3. Расчёт объёма видеопамяти

Графическая информация на экране монитора ПК представляется в виде изображения, которое формируется из точек (пикселей). Точка – область в месте пересечения воображаемых линий прямоугольной сетки, представляющая собой элементарный участок изображения, создаваемого компьютером на экране или принтером на бумаге.

Величину (измеряется в точках), определяющую количество информации, выводимое на экран монитора, называют разрешением экрана (разрешающей способностью). Разрешающую способность описывают две величины – число точек по вертикали и по горизонтали. Низкое разрешение, такое как 800 ´ 600, уменьшает область отображения и увеличивает отдельные элементы. Высокое разрешение, такое как 1024 ´ 768, увеличивает область отображения и уменьшает отдельные элементы. Для стандартных разрешений часто используются ещё и буквенные аббревиатуры (см. табл. 4.3).

Качество цветопередачи экрана монитора определяется числом цветов на точку, которое поддерживается монитором и графическим адаптером: 16 цветов (4 бита), 256 цветов (8 бит), 65 536 цветов (16 бит), 16 777 216 цветов (24 бита); 4 294 967 296 цветов (32 бита).

Таблица 4.3

Разрешающая способность мониторов

Для стандартных экранов (3:4)	Для широких экранов (16:9)
Поддерживаемый стандарт	Разрешение	Поддерживаемый стандарт	Разрешение
XGA	1024 ´ 768	WXGA	1280 ´ 800, 1366 ´ 768 или 1280 ´ 768
SXGA	1280 ´ 1024	WXGA+	1440 ´ 900
SXGA+	1400 ´ 1050	WSXGA+	1680 ´ 1050
UXGA	1600 ´ 1200	WUXGA	1920 ´ 1200

Так, для разрешающей способности экрана 800 ´ 600 точек, т. е. 480 000 точек, объём видеопамяти, требуемый для отображения 65 536 цветов, составит:

V = 2 байта ´ 480 000 = 960 000 байт = 937,5 Кбайт.

Аналогично рассчитывается объём видеопамяти, необходимый для хранения битовой карты изображений при других видеорежимах.

В видеопамяти компьютера хранится битовый план (bit map), являющийся двоичным кодом изображения, отсюда она считывается (не реже 50 раз в секунду) и отображается на экране.

Дата добавления: 2015-07-10