Цепи переменного тока. Рассмотрим цепь переменного тока

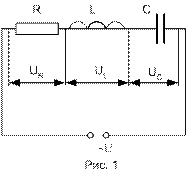Рассмотрим цепь переменного тока. Кроме сопротивления R, называемого активным, электрическая цепь в этом случае может обладать еще одним типом сопротивления, называемым реактивным сопротивлением. Последнее связано с наличием в цепи конденсаторов и катушек индуктивности. Соответственно различают реактивное емкостное и реактивное индуктивное сопротивления. Реальные элементы цепи обычно обладают одновременно и активным, и реактивным сопротивлениями. Если активное сопротивление много больше реактивного, то последним пренебрегают. Такой элемент цепи называют резистором. Существуют элементы цепи, обладающие только емкостным или только индуктивным сопротивлением. Элементы цепи, обладающие одним типом сопротивления, будем называть идеальными. В некоторых случаях реальный элемент цепи можно представить как комбинацию из нескольких идеальных.

Элементы электрических цепей подразделяют на линейные и нелинейные. Элемент называется линейным, если его сопротивление не зависит от силы протекающего тока или приложенного напряжения. Электрические цепи, составленные из линейных элементов, называются линейными. Электрические процессы, характеризующие такую цепь (рис. 1), описываются линейными алгебраическими или дифференциальными уравнениями.

Предположим, что внешнее напряжение U изменяется по закону синуса или косинуса:

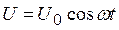(1)

(U₀ – амплитуда, ω – частота колебаний напряжения).

Оно равно сумме падений напряжения на каждом из элементов цепи R, L, C:

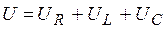(2)

Здесь

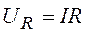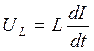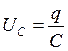, , , (3)

где R – сопротивление резистора,

L – индуктивность катушки,

C – емкость конденсатора,

q – заряд на пластинах конденсатора.

Заряд связан с током соотношением 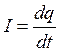. Соотношение (2) с учетом (3) и (1) приводит к дифференциальному уравнению

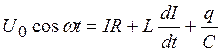, (4)

описывающему вынужденные колебания в цепи.

Решение этого уравнения имеет вид:

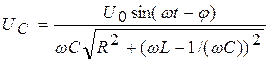(5)

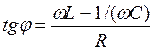. (6)

Умножив (5) на емкость С и продифференцировав полученное выражение по времени, найдем силу тока в цепи:

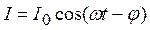, (7)

где

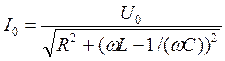. (8)

Сила тока отстает по фазе от напряжения на угол φ, который зависит от параметров цепи и частоты колебаний. Если φ <0, то происходит опережение силы тока от напряжения по фазе.

Выражение

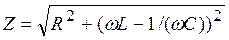, (9)

стоящее в знаменателе формулы (8), называется электрическим сопротивлением цепи, или импедансом.

Рассмотрим частные случаи.

1. Цепь содержит только активное сопротивление (L =0, C 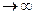). Тогда

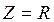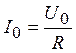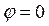, , . (10)

2. Цепь содержит только индуктивное сопротивление (R =0, C 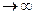). Тогда

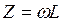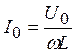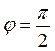, , , (11)

то есть сила тока в индуктивном сопротивлении отстает от напряжения на π /2. Величина X_L = ωL – реактивное индуктивное сопротивление.

3. Цепь содержит только конденсатор (R = L =0). Тогда

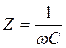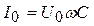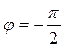, , , (12)

то есть сила тока, текущего через конденсатор, опережает напряжение на π /2. Величина X_C =1/(ωC) – реактивное емкостное сопротивление.

4. Реактивное сопротивление (R =0, но С 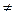0, L 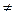0). Тогда

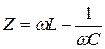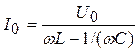, . (13)

Величина X = X_L - X_C = ωL -1/(ωC) называется полным реактивным сопротивлением.

Выражения (6) и (9) с помощью (14) переписываются в виде:

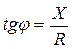, (15)

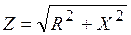. (16)

Дата добавления: 2015-07-10