И напряжения по толщине изоляции в кабеле переменного тока

Рассмотрим простейший случай. На рис. 2.2 изображен кабель с токопроводящей жилой радиусом r ₁ , радиусом по изоляции r ₂ ; между r ₂ и r ₁ находится изоляция. Напряжение U ₀ приложено между жилой и экраном, который находится на изоляции. Изоляция однородна (, объемные заряды отсутствуют (r = 0). Необходимо найти распределение напряжения U и напряженности E электрического поля между жилой и экраном. Воспользуемся уравнением Лапласа в цилиндрической системе координат:

Рис. 2.2. Распределение напря- женности электрического поля в изоляции кабеля

(2.10)

Напряжение по углу j не изменяется, поэтому

Вдоль кабеля по оси z напряжение также не изменяется, поэтому

Следовательно, уравнение (2.10) примет вид

(2.11)

Уравнение (2.11) справедливо в случае, если равно постоянной величине А:

(2.12)

Разделим переменные и проинтегрируем:

Выразим А:

(2.13)

Подставим А в выражение (2.12):

(2.14)

Преобразуем это выражение:

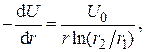
с учетом

окончательно получим

(2.15)

Из уравнения (2.15) следует, что напряженность электрического поля изменяется по гиперболическому закону, причем (из условия r ₁ < r ₂) максимальная напряженность будет на жиле (см. рис. 2.2):

(2.16)

а минимальная напряженность – на изоляции:

(2.17)

Возьмем выражение (2.14):

разделим переменные:

интегрируем:

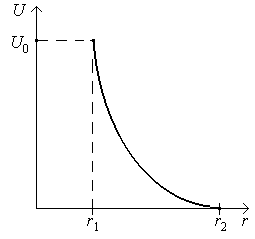
Рис. 2.3. Распределение напряжения в изоляции кабеля

Окончательно получаем

(2.18)

Из формулы (2.18) видно, что напряжение в изоляции кабеля изменяется по логарифмическому закону (рис. 2.3).

Дата добавления: 2015-07-12