Электрическое поле в кабеле

Для расчета электрического поля в кабеле применим теорему Остроградского – Гаусса, которая в интегральной форме имеет вид

(2.1)

т.е. поток (N)вектора электрического смещения (D) через замкнутую поверхность (S) равен сумме зарядов (q), расположенных в объеме, ограниченном этой поверхностью.

Теорема Остроградского – Гаусса связывает значения вектора электрического смещения в точках некоторой замкнутой поверхности с величиной заряда, находящегося внутри объема, ограниченного этой поверхностью. Можно придать этой теореме такую форму, чтобы в нее входили величины, относящиеся к одной и той же точке поля.

Введем прямоугольную систему координат x, y, z (рис. 2.1) и обозначим вектор электрического смещения в некоторой точке a(x, y, z) через

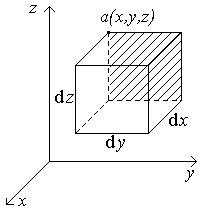D (D_x, D_y, D_z). Рассмотрим бесконечно малый прямоугольный параллелепипед с вершиной в точке a и ребрами d x, d y, d z. Поток через плоскость d y d z (заштрихована), проходящую через точку a, есть – (знак минус поставлен потому, что внешняя нормаль к плоскости d y d z и положительное направление вектора D_x составляют угол a = p и cos a= –1).

Поток через параллельную ей грань, смещенную вдоль оси x на d x, есть

Поток через обе грани

Рис. 2.1. Элементарный объем

где 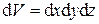– объем параллелепипеда.

Вычисляя аналогичным образом потоки через другие две пары граней и складывая их, мы получаем полный поток через всю поверхность параллелепипеда:

(2.2)

Если в рассматриваемом пространстве имеется распределенный в объеме заряд с объемной плотностью r, то величина заряда, содержащегося в объеме параллелепипеда, равна rd V. Приравняв поток вектора D к заряду, получим

или (2.3)

Это соотношение, выражающее теорему Остроградского – Гаусса в дифференциальной форме, носит название уравнения Пуассона – div D = = r, где

(2.4)

Предел отношения потока вектора через замкнутую поверхность S к величине объема V, ограниченного поверхностью S, при V ® 0 называется расхождением или дивергенцией вектора.

Используя выражение , получим

( 2.5)

Если диэлектрическая проницаемость не зависит от координат (, то уравнение Пуассона примет вид

( 2.6)

Нам предстоит решать общую задачу электростатики, т.е. по заданной форме проводников, их расположению и значению их потенциалов находить значение потенциалов в любой точке между проводниками. Математически эта задача сводится к следующему. Составляющие напряженности поля E по координатам можно выразить через потенциал:

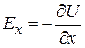или , , (2.7)

Подставив эти значения в уравнение Пуассона, получим

(2.8)

В изоляции кабелей нет свободных зарядов, поэтому

или . (2.9)

Это уравнение называется уравнением Лапласа.

Дата добавления: 2015-07-12