
|
Читайте также: |
(одна из возможных интерпретаций формального объекта)
t1 p2 t3
 | |||||





 ●
●
 |  | ||
 t2 p3
t2 p3
 | |||||||
 | |||||||
 | |||||||
 | |||||||
●
 p1 t4
p1 t4
 | |||
 |
T={t1, t2, t3, t4}
P={p1, p2, p3}
p1 – входное место для перехода t1
p2 – входное место для перехода t2
p3 – входное место для перехода t3
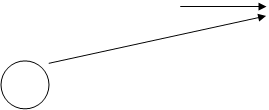
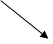
В данной интерпретации сеть Петри представляет собой размеченный вершиновзвешенный мультиграф со множеством вершин. Из вершины-места, изображаемой кружком, ведет дуга в вершину-переход, изображаемый прямоугольником, тогда и только тогда, когда функция инцидентности F(pi, tj)=1. Из вершины-перехода в вершину-место ведет дуга, когда функция инцидентности F(tk, pl)=1. Место помечается разметкой. При этом часто эта разметка является числом точек (фишек) внутри кружка (M0 (pt) # 0).
Динамика поведения моделируемой системы, рассматриваемая в терминах функционирования сети Петри.
Сеть функционирует в дискретные времена, переходя от разметки к разметке. При этом разметка – это функция M: P → {0, 1, 2, 3,… } смены разметок (начиная с М0), происходящей в результате срабатывания перехода в сети Петри. Переход может сработать при разметке М, если для любого р имеет место неравенство
tq ∈ T, pt ∈ P, M(p) – F(p,t) ≥ 0
Т.е., если каждое его входное место имеет хотя бы одну фишку и в результате срабатывания перехода при заданной разметке М, последняя сменяется разметкой М' по правилу
∀ P ∈ P, M'(p) – F(p,t) + F(t,p)
Т.е. переход Т изымает по фишке из каждого своего места и посылает по фишке в каждое свое выходное место. Если может сработать несколько переходов, срабатывает один. Сеть останавливается, если при некоторой разметке (тупиковой) ни один из ее переходов не может сработать. При одной и той же начальной разметке сеть Петри может порождать (в силу недетерменированности ее функционирования) различные последовательности срабатывания ее переходов. Эти последовательности образуют слова в алфавите Т, а множество всевозможных слов, порождаемых сетью Петри, называются ее языком.
Две сети Петри эквивалентны, если они порождают один и тот же язык.
Замечания.
1. В отличие от конечных автоматов, в терминах которых описывают глобальные изменения состояния систем, сети Петри концентрируют внимание на локальных событиях (им соответствуют переходы), локальных условиях (им соответствуют места), локальных связях между событиями и условиями. Поэтому в терминах сетей Петри более адекватно, чем с помощью языка конечных автоматов, моделируется поведение распределенных асинхронных систем.
2. Как математическая модель сеть Петри занимает место между конечными автоматами и машинами Тьюринга. При этом по выразительной возможности язык сети Петри значительно богаче языка конечных автоматов и приближается к машине Тьюринга.
3. Немаркированная сеть Петри, т.е. сеть, где М=0, есть статичная структура.
4. Последовательность запуска переходов – выполнение сети Петри.
Пример1. Рассмотрим выполнение сети Петри, заданной мультиграфом.



 t2 p1
t2 p1


 ●
●
 | |||
 | |||
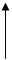
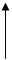
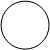 t3
t3




 ● t1
● t1



 p2
p2



 p3
p3


 t4 p4
t4 p4
 p5
p5
_
G=<V, U>
V=T ∪ P
|T|=4, |P|=5, |V|=9
M0 = <1,0,1,0,0>
M' = <1,1,0,0,0>
M" = <0,1,1,0,0>
Пример2. Рассмотрим выполнение сети Петри, заданной мультиграфом.
 p1 p4
p1 p4
 |  |  |  | ||||
● ●

 t1 t2
t1 t2
 |


 p2 p3 p5
p2 p3 p5
●
 |  | ||||||
 |  | ||||||
 t4 t3
t4 t3
 |  |  | |||||||||
 |  |  |  |
|T|=4, |P|=5, |V|=9, M0=<1,0,1,1,0>
Решение
t1
M0 ├── M1=<0,1,0,1,0>
t4
M1 ├── M2=<0,0,1,1,0>
t2
M2 ├── M3=<0,0,0,0,1>
t3
M3 ├── M4=<0,0,1,0,0>
Дата добавления: 2015-07-10; просмотров: 80 | Нарушение авторских прав