Частичные автоматы.

Логическая функция f: Bⁿ → B, где В={0,1}, заданная на числе наборов булевых кортежей меньших 2ⁿ (где n – число аргументов логической функции), называется частично определенной логической функцией, т.е. это такая логическая функция, которая на некоторых наборах не определена.

Очевидно, что если функция n аргументов не определена на m двоичных кортежах (m<n), то такая логическая функция может быть доопределена 2^m способами. Такое до определение необходимо для того, чтобы логическую функцию можно было задать аналитически в виде канонических форм.

Пример. Пусть задана логическая функция трех аргументов

	F(x1x2x3) = V F(1^*,2,3^*,4,5,7^*)

В этом примере логическая функция не определена на 1,3,7 наборах. Если функцию до определить нулями, то в результате минимизации получится новая функция

	_ _ _ F(0)= x1x2 ∨ x1x2x3

Если функцию до определить единицами, то новая минимальная функция имеет вид

	_ _ F(1)=x3 v x1x2 ∨ x1x2 _ _ Fmin(x1x2x3)=x1x2 ∨ x1x2

Замечания.

1. Среди восьми до определенных логических функций минимальный автомат имеет наименьшее число букв.

2. До определение логической функции существенно влияет на конечный результат минимизации.

3. При до определении функций руководствуются следующим правилом:

МДНФ не полностью определенной логической функции получается как дизъюнкция наиболее коротких по числу букв импликант функции, принимающих значение единицы на всех кортежах частичной функции, которые в совокупности покрывают все импликанты СДНФ для частичной функции, принимающей значение нуля на всех кортежах, где она не определена.

Пример. Синтезировать одноразрядный двоичный сумматор с использованием свойств не полностью определенных логических функций.

Описание поведения двоичного сумматора задаем таблицей соответствия.

ai	bi	ni-1	ci	ni

a_i, b_i – слагаемые i-го разряда операндов a, b

c_i – сумма a_i + b_i

n_i, n_i-1 – переносы из i (i-1) разрядов.

Минимальная форма логической функции имеет вид

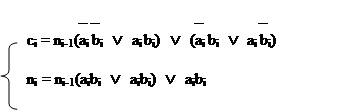Этот результат можно получить и путем минимизации не полностью определенной логической функции вида

с^*=f^*(a_i, b_i, n_i-1, n_i)

Таблица соответствия такой логической функции имеет вид (строим с учетом исходной таблицы соответствия, задающей поведение автомата).

a_i b_i n_i-1 n_i

&

&

a_ib_i

O

&

(a_i ∨ b_i) n_i-1

ai	bi	ni-1	ni	ci^*	№ пп
				*
				*
				*
				*
				*
				*
				*
				*

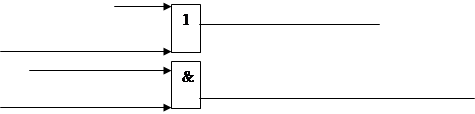
До определение функции c_i^*

	ci^*(1)=V F(1,2,3,4,5,6,8,9,10,12,14,15) ci^*(0)=V F(2,4,8,15)

Минимизируя имеем следующую минимальную форму для

	_ _ _ _ _ _ _ _ сi^*(1)=ai ni ∨ bi ni ∨ ni-1 ni ∨ ai bi ni-1 ∨ ai bi ni-1 ∨ ai ni-1 ni ∨ ai bi ni-1

Таблица покрытий для функции c_i^*(0) имеет вид

Первичные	Исходные термы
импликанты	_ _ _ ai bi ni-1 ni	_ _ _ ai bi ni-1 ni	_ _ _ ai bi ni-1 ni	ai bi ni-1 ni
_ ai ni			√
_ bi ni		√
_ ni-1 ni	√
ai bi ni-1				√
_ _ ai bi ni-1			√
_ _ ai ni-1 ni
_ _ ai bi ni-1	√

Минимизация покрытия позволяет записать окончательный вид уравнения

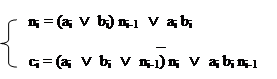Дата добавления: 2015-07-10