Классификация конечных автоматов.

⇐ ПредыдущаяСтр 2 из 11Следующая ⇒

Читайте также:

1. В том случае, когда S всюду определено, то говорят (и пишут) о полном недетерминированном автомате.

U=< A, Q, B, Г >

Dom Г = Q x A

Im Г Í Q x B

2. Если S_fn: QxA→Q является однозначным, то говорят о конечном частичном детерминированном автомате (по переходам).

U=<A, Q, B, S_fn>

Dom S_fnÌ QxA

| i_m q_ia_j| ≤ 1

f_n – функция перехода.

3. Конечный автомат называют частичным детерминированным по выходам, если

S_fb: QxA→B является однозначной.

U=<A, Q, B, S_fb>

Dom S_fbÌ QxA

| i_m q_ia_j| ≤ 1

4. Конечный автомат называют частично детерминированным по переходам и выходам, если S_f₁: QxA→Q и S_f₂: QxA→B функциональны

Dom S_fÌ QxA

| i_m q_ia_j| ≤ 1

5. Всюду определенный синхронный детерминированный по переходам и выходам конечный автомат называют автоматом Мили (автомат первого рода).

U=<A, Q, B, δ, λ>

δ: QxA→Q

λ: QxA→B

В этом случае поведение такого синхронного автомата может быть записано парой уравнений

q_l (t) = δ (q_j (t-1), a_i (t)) b_p (t) = λ (q_j (t-1), a_i (t))

t = 1,2,3,…

Примечания для автомата второго рода

{

q_l (t) = δ (q_j (t-1), a_i (t)) b_p (t) = λ (q_j (t), a_i (t))

t = 1,2,3,…

2. Для каждого автомата второго рода существует эквивалентный ему абстрактный автомат первого рода, функция выходов которого получается в результате подстановки(суперпозиции) функции переходов автомата второго рода в его сдвинутую функцию выходов.

λ₁(q_j_, a_i) = λ(δ(q_j_, a_i), a_i)

3. Частным случаем автомата второго рода является автомат Мура, закон функционирования которого задается

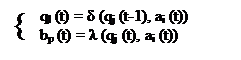Пример. Пусть заданы кортежи

<q₀, a₁> → < q₂, b₁>

<q₁, a₂> → < q₃, b₂>

<q₁, a₃> → < q₂, b₁>

4. Для любого автомата Мили существует эквивалентный ему автомат Мура и наоборот. Любой автомат Мура путем добавления ряда внутренних состояний может быть преобразован в автомат Мили.

5. Конечный автомат называется инициальным, если среди внутренних состояний этого автомата выделено одно, так называемое, начальное состояние.

6. Автомат называется асинхронным, если в нем для любого внутреннего состояния и для любой входной буквы функции переходов не изменяются.

δ (q_i, a_j, a_j, a_j, a_j,_…, a_j) = δ (q_i, a_j)

Состояние q_i называется устойчивым по входному символу a_j.

Модель асинхронного автомата отражает поведение автомата, внутреннее состояние которого может меняться лишь при изменении входных символов. (В отличие от синхронного автомата, в котором состояние меняется при подаче слова из одинаковых букв).

7. Автомат Мили, для которого функция выхода не зависит от внутреннего состояния, называют комбинационным или тривиальным.

В комбинационном автомате все внутренние состояния эквивалентны.

Минимальный комбинационный автомат – автомат без памяти. В этом случае минимальный автомат есть

U=<A, B, δ, λ>, |Q|=1

8. Автомат Мили называется автономным автоматом, если мощность множества А равна единице.

U=<Q, B, δ, λ>, |A|=1

Входные слова для автономного автомата имеют вид цепочки из одной и той же буквы, а таблицы переходов и выходов состоят из одного столбца.

9. Автомат Мили называют логическим, если его входной алфавит состоит из 2^m двоичных наборов длиной m и выходной алфавит состоит из 2^k двоичных наборов длиной k. Очевидно, что для логического комбинационного автомата функция переходов вырождена, а его поведение однозначно определяется функцией выходов с одним аргументом.

10. Автоматом без выходов называют такой автомат Мили, у которого мощность множества В равна единице.

Замечания.

Автомат Мура можно рассматривать как автомат без выходов, состояния которого различным образом отмечены.

Конечный автомат называют минимальным, если среди автоматов, реализующих заданный атоматный оператор T: A^* → B^* он имеет наименьшее возможное число внутренних состояний.

Конечный автомат называют последовательностным (автомат с памятью), если его выход зависит не только от входных символов, но и от предистории (как выходных, так и входных символов).

Очевидно, что разновидностью последовательностных автоматов являются синхронный и асинхронный автоматы.

11. Конечный автомат называют нечетким, если функция его реакции есть нечеткое отношение.

} нечеткий автомат } четкий автомат

QxAxQ → [0,1]

QxAxB → [0,1]

QxAxQ → {0,1}

QxAxB → {0,1}

12. Автономный автомат Мура называют генератором. Иначе генератор – это конечный автомат, для которого |A|=1, а λ: Q→B, λ (q).

13. Конечный автомат называют вероятностным, если его начальное состояние – случайное состояние, а функции переходов и выходов тоже случайны.

14. Конечный инициальный автомат с поведением вида

R_fÍ A^*, F Ì Q

R_f = {α Î A^*; δ(q₁, α) Î F}

называют акцептором.

R_f – событие

α – слово

А^* - А ∪ А² ∪ А³ ∪ … Аⁿ ∪…

F – заключительное состояние

q₁ – начальное состояние.

Конечный инициальный автомат с поведением вида А^*→В^* называют преобразователем.

Пример определения множества состояний по внутренней структуре объекта.

На вход источника поступают импульсы со значениями "0", "1" со скоростью один импульс в каждую τ секунду. Тактовые моменты выбраны совпадающими с моментами появления импульсов. Элементы D1, D2, D3 – задержки, которые запоминают поступающие на их вход импульсы и передают их на следующие за ними элементы. Элемент ξ выдает импульсы"0" или "1" в зависимости от значения, соответствующего большинству поступающих на его входы импульсов.

А=В={0,1}, Q={<0,0,0>, <0,0,1>, <0,1,0>, …}

Будем рассматривать предложенную схему как конечный автомат (автомат Мили – синхронный логический автомат с памятью)

	q(t)	q(t+1)
A	D1(t)	D2(t)	D3(t)	D1(t+1)	D2(t+1)	D3(t+1)

Приведенная таблица полностью описывает поведение рассмотренной схемы. Из этой таблицы легко определить, что при q(t)={0,0,1} и входном сигнале a=1 q(t+1)={1,1,0}.

Замечание (Теорема).

1. Для неинициального нетривиального комбинационного автомата с одним состоянием его реакцию предсказать нельзя (это можно определить только для инициального автомата).

2. Граф поведения рассматриваемого автомата имеет восемь состояний.

0,0 0,0