Формула 8.4. Вычисление угла между наблюдателем и объектом.

Если мы зададим вектор направления взгляда, как V, а вектор скорости, как О, тогда угол между ними можно будет найти по следующей формуле:

Пусть V = (vx,vy,vz) и О = (ox,oy,oz), тогда

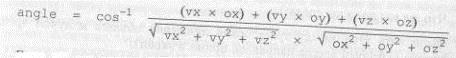
Если бы мы хотели сформулировать это действие словами, то могли бы сказать так: «Угол между V и О равен арккосинусу скалярного произведения этих векторов, разделенного на произведение длин векторов».

Угол между V и О, рассчитанный по этой формуле, имеет одну особенность: он всегда внутренний, то есть больше 0, но меньше 180 градусов. Следовательно, один и тот же результат, полученный по этой формуле, может соответствовать двум разным углам. Это происходит потому, что скалярное произведение не дает информации о направлении вектора (или о направлении, в котором вы отсчитываете положительный угол). Другими словами, эта формула всегда выдает наименьший из углов между двумя векторами. Если вы будете помнить об этом, то такое поведение данной формулы не будет большой проблемой. (Это напоминает бутерброд, который всегда падает маслом вниз. Если вы не знаете об этом, то такой результат может свести вас с ума. А кто предупрежден, тот вооружен.)

Рисунок 8.9 иллюстрирует указанную проблему графически. На этом рисунке показан вектор направления взгляда, три возможных положения вектора траектории и полученный в результате расчетов по формуле 8.4 угол.

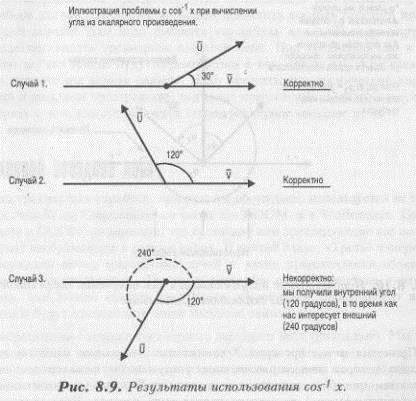
Кстати, формулу 8.4 можно значительно упростить, вспомнив, что нас интересует только плоскость X-Z, так как луч зрения всегда перпендикулярен плоскости просмотра.

Но как же, в конце концов, определить действительный угол? Конечно, вы Могли бы воспользоваться еще и векторным произведением, чтобы решить, корректен ли угол, полученный в результате расчетов по формуле 8.4 или необходимо увеличить его еще на 180 градусов. Однако я слишком не люблю математику (возможно, именно поэтому я и доктор математических наук) и предпочитаю вместо грубой силы использовать тонкую интуицию.

Если мы сообразим, что вектор траектории объекта имеет ту же исходную точку, что и вектор направления взгляда, а затем проверим, в какой из полуплоскостей относительно луча зрения расположен Х-компонент вектора траектории, то мы сможем определить, больше или меньше 180° искомый угол. Это наглядно изображено на рисунке 8.10.

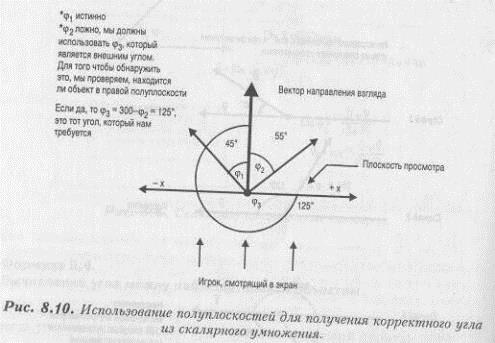
Применяя метод проверки Х-компонента, мы можем написать простую функцию, которая вначале рассчитывает угол, используя скалярное произведение, а затем проверяет, находится ли координата Х справа (положительная) или слева (отрицательная) от вектора направления взгляда. Если координата Х положительная, мы вычитаем угол, полученный с помощью формулы 8.4 из 360 градусов (это все равно, что прибавить 180). Затем мы можем взять рассчитанный угол и разбить его на 12 квадрантов (либо взять его модуль по основанию 12). Полученное число затем можно использовать как индекс для нахождения кадров спрайта. (Конечно, кадры должны быть расположены в правильном порядке, то есть кадрам, полученным при вращении объекта против часовой стрелки с шагом в 30 градусов, должны соответствовать индексы от 0 до 11. При этом нулевой индекс должен указывать на кадр объекта, повернутого тыльной стороной к наблюдателю.)

Если значение координаты Х отрицательное, происходит то же самое за исключением того, что будет использован другой банк изображений, и оперировать потребуется с абсолютным значением X.

Кадры, которые я создал для демонстрации этого алгоритма, расположены в файле VRYENTXT.PCX. Они расположены слева направо и сверху вниз. Каждая картинка содержит изображение, повернутое на 30° против часовой стрелки, а в исходной позиции нос корабля направлен прямо в экран (или, с точки зрения игрока, корабль обращен к нему тыльной стороной). Этот же файл мы использовали и в предыдущем примере.

Демонстрационная программа будет использовать рассчитываемые углы для выбора кадров. Но мы же не можем поместить корабль просто в пустоту. Это будет скучно! Нам надо добавить что-нибудь для оживления картинки. Я предлагаю создать трехмерное звездное небо. Под трехмерностью я здесь понимаю то, что звезды будут перемещаться к вам или от вас, а не влево или вправо, как это мы делали раньше, Надо отметить, что космический корабль, летящий в звездном пространстве, выглядит превосходно. Однако следует еще поговорить о том, как же создается такое трехмерное звездное небо.

Трехмерное звездное небо

Техника трехмерных спрайтов, которую мы обсуждаем, используется не только в играх типа Wing Commander, но также и в DOOM, и в Wolfenstein. Если вы поиграете в DOOM, то заметите, что гуляющие или преследующие вас монстры (спрайты) изображаются в разных видах. В шестой главе, «Третье измерение», мы обсуждали метод трассировки лучей и метод представления объектов с помощью многоугольников. Теперь я хотел бы снова вернуться к этому и показать, как можно создать трехмерное космическое пространство внутри которого и будут происходить наши звездные войны.

Теоретически создание трехмерного звездного неба тривиально. Мы могли бы просто задать несколько миллионов случайных точек в трехмерном пространстве, использовать аксонометрическую проекцию для их визуализации и, нарисовать их по пикселям. Этот метод волне применим и обычно используется в симуляторах. Однако у него есть ряд недостатков: он работает медленно, требует много памяти и получаемое в результате изображение быстро надоедает из-за своего однообразия. Но поскольку мы с вами сейчас занимаемся оформлением игры, то должны сделать так, чтобы экран действительно стал трехмерным звездным небом. Но мало сказать, надо еще и сделать! Если вы найдете время и посмотрите Star Trek или подобный симулятор, то увидите звездное небо, созданное с помощью одиночных пикселей (звезд). Эти звезды расположены на экране случайным образом и передвигаются к периферии вначале медленно, а потом все быстрее и быстрее. Это происходит до тех пор, пока звезды не будут отсечены, выйдя за пределы обозримого пространства.

Реализм

Чтобы небо выглядело более реалистично, звезды, находящиеся на меньшем расстоянии от корабля, на котором, мы летим (от нашей виртуальной точки обзора), должны светить ярче. Я предлагаю следующий алгоритм создания трехмерного звездного неба:

1. Для описания звезды создать структуру, содержащую информацию о ее расположении, цвете и скорости перемещения;

2. Создать массив звезд, расположенных по всему экрану и движущихся с разной скоростью;

3. Сделать так, чтобы звезды двигались из центра экрана к краю;

4. Сделать так, чтобы за каждый <?тик» таймера звезда немного ускорялась и становилась ярче;

5. Сделать так, чтобы, достигнув границы экрана, звезда появлялась вновь в иной случайной позиции и перемещалась с другой скоростью;

6. Нарисовать звезды;

7. Вновь вернуться к пункту 4.

Этот метод позволяет получить очень натурально выглядящие звезды и достаточно просто осуществляется. Однако и он тоже не лишен недостатков:

§ Во-первых, вы не можете повернуть и должны всегда двигаться вперед;

§ Во-вторых, начальная скорость звезды может быть слишком велика по отношению к скорости объекта, летящего по звездному небу.

Первая проблема действительно серьезная..Если по сценарию игры вам требуется изменять направление полета, то надо воспользоваться каким-нибудь другим алгоритмом. Вторая же проблема, по моему мнению, чисто академическая. Кого волнует, что наш корабль летит со скоростью, во много раз превышающей световую? Это игра, и мы вольны строить такую вселенную, какая нам больше нравится!

Создание звездного неба с использованием целых чисел

Теперь поговорим о том, как можно создать звездное небо используя только целые числа. Мы могли бы для получения более точной картины использовать числа с плавающей запятой, такие, например, как 2,5. Однако мы знаем, что это снижает производительность системы. Нам же требуется создать и визуализировать 50-100 звезд как можно быстрее, чтобы остальное время работы процессора потратить на масштабирование спрайтов и развитие сюжета игры.

Если создавать звездное небо, привлекая только целые числа как значения скоростей звезд, то едва ли вы заметите количественную ошибку, обусловленную заменой чисел с плавающей запятой на целые.

Конечно, мы могли бы принять компромиссный вариант и использовать числа с фиксированной запятой, но в данном случае овчинка выделки не стоит. Я считаю, что при достаточно высоких скоростях звезд потеря дробной части числа несущественна. Наверное, я уже утомил вас, повторяя одно и то же: в компьютерных играх все и всегда должно быть реализовано самым простым и быстрым путем. С другой стороны, такое примитивное на первый взгляд оформление игры, как экран, усыпанный звездами, может отнять у программиста удивительно много времени и сил. Но не забывайте, что отличное оформление - залог того, что игрок погрузится в игру с головой!

Листинг 8.3 содержит полный текст программы, позволяющей перемещать космический корабль по трехмерному звездному небу (отметим, что сам звездолет находится в плоскости X-Z). Для перемещения корабля используется вспомогательная цифровая клавиатура. Клавиши Left и Right вращают корабль, а клавиши Up и Down замедляют и ускоряют его движение. Для выхода из.программы нажмите клавишу Q.

При компоновке исполняемого файла вы должны объединить модуль FINVYREN.C с графической библиотекой GRAPHICS.С.

Дата добавления: 2015-07-12