Формула 8.2. Расчет масштабирования.

scale=scale_distance/sprite_z,

где scale_distance расстояние - визуально дающее хороший результат.

Мы знаем, что создание трехмерной графики не может быть легким делом с ней надо повоевать! И мне это даже нравится! Существует еще одна небольшая проблема - отсечение. И большая часть этой главы посвящена именно этой проблеме.

Видимый объем

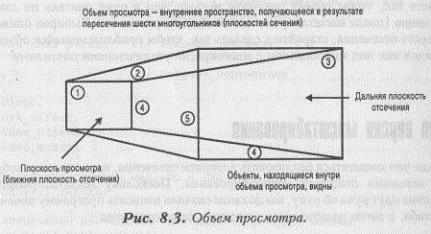
Как мы узнали в главах, посвященных трехмерной графике, базирующейся на многоугольниках (глава шестая, «Третье измерение» и седьмая, «Улучшенная битовая графика и специальные эффекты»), объекты должны быть отсечены в пределах видимого объема (или усеченной пирамиды просмотра). Это достигается путем определения ребер каждого многоугольника и отсечения их шестью гранями видимого объема. Возникающая при этом проблема состоит в том, что объем просмотра представляет собой трехмерный трапецоид, состоящий из шести интересующих нас плоскостей, так как это показано на рисунке 8.3.

Мы, конечно, не хотим рассчитывать пересечения спрайтов с произвольными плоскостями. Это было бы уж слишком! Но если мы вначале спроецируем каждый спрайт в аксонометрии и рассчитаем их масштаб, то сможем превратить объем просмотра в прямоугольник. Теперь, так как мы выполняем обратную операцию, мы сможем отсечь спрайты куда как более легким образом, чем при использовании уравнений произвольных плоскостей.

Этот прием основывается на том факте, что объем просмотра уже является аксонометрической проекцией. Если мы отсечем края трехмерного объекта? видимым объемом прежде, чем спроецируем этот объект, мы будем обязаны использовать трапецеидальные формы объема просмотра. Однако, если мы вначале спроецируем объект с учетом перспективы, а затем отсечем его прямоугольными границами видимого объема, то.результат, полученный таким образом, будет полностью совпадать с результатом, достигаемым первым способом. Отсечение же в плоскостях, параллельных плоскости просмотра, сводится к простому условному оператору, в котором проверяется, является ли спрайт слишком далеким или слишком близким по отношению к вам.

В случае видеорежима l3h мы можем отсекать все спрайты по размерам экрана или четырехугольника, границы которого определяют точки (0,0) и (319,199). Отсечение в плоскостях, параллельных плоскости просмотра, осуществляется с помощью простого теста на выполнение условия: если спрайт находится внутри наблюдаемого Z-пространства, то визуализируйте объект, а в противном случае игнорируйте его. Отсечение в этих плоскостях выглядит так просто оттого, что в действительности спрайты — это прямоугольные многогранники, расположенные перпендикулярно линии взгляда, или параллельно плоскости просмотра (вы можете думать, как вам больше нравится, но на самом деле это одно и то же).

Я полагаю, что, поэкспериментировав с отсечением дальней плоскостью, вы сделаете так, чтобы объект размером меньше, чем в один пиксель по любому измерению (после масштабирования) вообще не рисовался. Выбирая ближнюю плоскость отсечения, старайтесь сделать так, чтобы приближающийся объект не выглядел как под микроскопом с многократно увеличенными пикселями.

Новая версия масштабирования

Прежде чем попытаться реализовать алгоритм отсечения, мы должны разобраться с основами операций масштабирования. Поскольку масштабирование и отсечение идут рука об руку, мы должны сначала написать программу изменения масштаба, а затем адаптировать ее для процесса отсечения.

Механизм масштабирования мы показали в седьмой главе, «Улучшенная битовая графика и спецэффекты» (Листинг 7.9). Для масштабирования текстуры стен в этом алгоритме был использован не совсем обычный подход. Каждая стена рассматривалась не как обычная двухмерная матрица, имеющая высоту и ширину, а разбивалась на отдельные одномерные столбцы. В результате программе нужно было масштабировать только столбцы шириной в один пиксель. (Кстати, простой текстурированный пиксель называется текстелем (textel).)

Для реализации двухмерного масштабирования мы слегка модифицируем код, представленный в Листинге 7.9. В новом варианте будут использованы только целые числа, а индексы масштабирования будут предварительно подсчитаны и занесены в таблицу соответствий. Текст новой программы масштабирования приведен в Листинге 8.1.

Дата добавления: 2015-07-12