Высокоскоростные трехмерные спрайты

На самом деле, новых понятий в этой главе не появится. Скорее, речь пойдет о практическом применении тех технологий и концепций, которые мы обсудили в предыдущих главах. Обычно я никогда не рассматриваю практическую реализацию в книгах подобного плана. Это связано с тем, -что создание программы - скорее, творческий, чем технологический процесс. Однако в данном случае я изменил свое решение, так как хочу, чтобы вы четко разобрались в ряде основополагающих концепций.

За последние несколько лет мир компьютерных игр пережил несколько сенсаций (и появление игры DOOM одна, но не единственная, из них). К этим сенсациям, в том числе следует, отнести и появление на свет игры Wing Commander, написанной Крисом Робертсом (Chris Roberts). Увидев ее впер вые, я был так потрясен, что вскоре она стала моей любимой игрой. В Wing Commander и других играх подобного плана была использована та же технология визуализации спрай тов, что и в играх типа DOOM,

Образы в Wing Commander - это или простые макеты, или создаваемые компьютером объекты, преобразованные в цифровую форму двухмерного спрайта.. При движении по экрану эти спрайты видоизменяются по определенным математическим законам, создавая полное ощущение перспективы. Однако, хотя с формальной точки зрения данные изображения и не являются трехмерными, над ними производятся стандартные процедуры удаления невидимых поверхностей и другие математические расчеты для трехмерных изображений. Другими словами, это проекции трехмерных объектов на плоские многоугольники, которые собственно, и являются спрайтами.

Для изготовления игры типа Wing Commander не требуется сверхсложной математики. Однако подобная игра содержит массу тонкостей, хитрых приемов и замечательных алгоритмов. Посмотрим, сможем ли мы разобраться в некоторых из них, обсудив следующие вопросы:

§ Механика трехмерных спрайтов;

§ Аксонометрические преобразования;

§ Правильный расчет масштаба;

§ Видимый объем;

§ Новая версия масштабирования;

§ Отсечение в трехмерном пространстве спрайтов;

§ Построение траекторий;

§ Удачный угол зрения на спрайты;

§ Трехмерное звездное небо;

§ Оцифровка объектов и моделирование;

§ Создание съемочной студии;

§ Цветовая палитра.

Механика трехмерных спрайтов

Трехмерные спрайты очень похожи на двухмерные. По правде говоря, они и являются плоскими, просто нам кажется, что они объемные. Такое восприятие обуславливается тем, как они движутся по экрану и как при этом изменяется их размер- Двухмерные спрайты могут перемещаться только по осям Х и У, трехмерные же должны перемещаться ло всем трем осям — X, У и Z. Движение вдоль оси Z, фактически, осуществляется только в математическом плане за счет изменения координат спрайта одновременно по осям Х и Y, а также вычислением его размера, определяемого координатой Z. Именно это и делает плоские картинки похожими на трехмерные.

Конечно, мы опустили некоторые детали. Как может плоское изображение выглядеть трехмерным? Чтобы ответить на этот вопрос, нарисуем объект так; как бы он выглядел под определенным углом зрения в пространстве. В качестве

примера к этой главе, я заснял на видеокамеру вращение игрушечного космического корабля, а затем оцифровал полученные кадры. Для этого я закрепил камеру и объект на определенном расстоянии друг от друга, как показано на рисунке 8.1, и для каждого снимка чуть-чуть поворачивал игрушку вокруг вертикальной оси. Таким образом, я получил 12 кадров, которые изображали корабль под разными углами. Эти кадры приведены на рисунке 8.2. Если мы последовательно отобразим их на экране, то получим иллюзию вращающегося в сотне шагов от нас космического корабля.

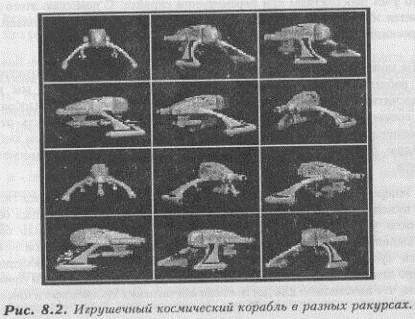
Трехмерный вид спрайтов обуславливается двумя различными факторами:

§ Во-первых, мы сканируем (или рисуем) объект в различных ракурсах. В конечном счете, лучше всего получить изображение во всех возможных позициях вращения, но это не получится из-за того объема памяти, необходимой для хранения всех изображений. Например, для этой главы я создал спрайты размером 80х48 пикселей. Это значит, что каждое изображение требует 3840 байт. На первый взгляд эта величина не кажется слишком большой, но только до тех пор, пока вы не подсчитаете объем памяти, занимаемый всеми кадрами, выполненными под разными углами зрения. Если мы хотим просто вращать объект относительно оси Y с шагом в 30 градусов и рассматривать его с 4 разных уровней высоты, на это уйдет 12х4х3840=184К. А теперь представим, что нам понадобились изображения большего размера либо несколько подобных изображений (или и то и другое сразу)! Для экономии памяти можно оцифровывать только некоторые из требуемых изображений, а недостающие получать преобразованием имеющихся по мере необходимости. Например, можно нарисовать виды объекта только под углами зрения в пределах от 0 до 180 градусов, а для оставшихся 180 градусов получать изображение из исходного набора данных уже программным путем;

§ Второй фактор, с помощью которого достигается иллюзия трехмерности это учет перспективы при перемещении спрайта. С помощью этого достигается эффект передвижения объектов вперед и назад относительно точки проекции и горизонта.

Мы можем считать, что спрайты - это точки в трехмерном пространстве и работать с ними на основе этого предположения. Тогда мы можем рассчитывать коэффициенты их масштабирования и строить изображение в соответствии с расстоянием до них от наблюдателя (то есть от вас), Наконец, во время перемещения спрайтов по экрану мы должны выбирать кадры, соответствующие углу наблюдения, под которым они рассматриваются.

А теперь поговорим о том, как поддерживать иллюзию объемности. Если игрок, путешествуя по игровому пространству, заходит за трехмерный объект, он должен увидеть его сзади, а отнюдь не с боку, как это было бы при перемещении слева направо. Учет этого обстоятельства основывается на отслеживании траектории объекта и вектора взгляда игрока. Мы обсудим это подробно немножко позже в настоящей главе, а сейчас я просто хотел упомянуть обо всем, что необходимо для достижения впечатления трехмерности при работе со спрайтами.

Аксонометрические преобразования

Мы уже говорили об этом раньше (в шестой главе, «Третье измерением). Для воспроизведения объектов на экране компьютера используются аксонометричес кая проекция и связанные с ней математические преобразования, так как эта проекция выглядит более реалистично, чем параллельная (ортогональная). При построении аксонометрической проекции значения координат Х и Y модифицируются с учетом координаты Z (то есть расстояния от наблюдателя до плоскости просмотра, которой в нашем случае является экран), создавая тем самым иллюзию реальной перспективы.

Для правильного аксонометрического преобразования трехмерного спрайта мы должны использовать его центр в качестве его позиции или локального центра координат. Это весьма важно! Если мы будем за центр координат принимать верхний левый угол спрайта (как мы это делали раньше), то получим искаженную картину. Всегда в качестве локального центра координат используйте середину объекта. Необходимость этого вызвана тем, что образ должен масштабироваться равномерно от его центра, а не от верхнего левого угла. (Запомнили? Повторите. Отлично!)

Дата добавления: 2015-07-12