При одинак темп сред квадр скор мол кисл Меньше сред кв водор.

Распр Ма-Бо:

потенциальная эн частиц во внеш поле плюс сум кин энергия мол
Распределение электронов по состояниям

Размерность статистического веса: безразмерная величина

Распределение электронов по энергиям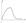

Распределение Больцмана по состояниям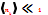

Распределение Больцмана по состояниям

Распр Боль f(E)= сист частиц мал плот, у которых не прояв кван св

Распр Макс по мод скор для Т₁>Т₂ показано на рис: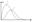

Распределение фононов по состояниям имеет вид:

Реальные процессы в изол: в направ увел хаот движ частиц в системе

Распр Бозе-Эйн по эн –сред число бозонов в един малом интер эн

Система фононов описывается статистикой Бозе-Эйнштейна

Согласно теореме о равнораспределении эн равно:

Среднее значение для одноат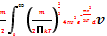

Среднее значение для молекул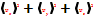

Среднее значение 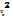можно найти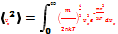

Статический вес системы: зависит от числа частиц системы

Средние скорости молекул T₁=T₂, m₁>m₂: <v₁> < <v₂>

Случайная вел х принимает значения от 0 +∞. f(x)=Ce^-bx b

Температура вырождения системы T_в. Для невыр Т>>Т_в

Теплоём электрон газа в металлах 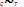т.к. средняя энергия

теплового движения электронов в металле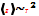

Темп абсол черного тела Т=10³ К. Вина В=6*10¹⁰ 1/с*К. 6*10¹³ Гц

Термодинамическая сист наход в равновесном сост: E=const, S=S_max

Теплоемкость общей массы идеального одноат V=const: C=3R

Точка в фазовом пространстве для системы из N: микросостояние системы

Услов норм функ Макс по мод скор: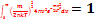

У изолированной системы, находящейся в равн сост: Ω=Ω_min

Функция распределения Ферми-Дирака по состояниям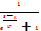

Функ распр Фе-Дир по сост средн число фермионов в одном кв сост

Функция распределения Ферми-Дирака по эн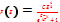

Функ распр мол по проекции скор v_x, пронорм на 1,:

Функция распределения Фер-Дирака по эн при Т=0

Функция распр Макс по мод скор (плотность вероятности) f(υ):

относительному числу молекул в единичном интервале скоростей

Дата добавления: 2015-07-10