Пункт 10.

Считая, что стенки трубы выполнены из реального метла, имеющего σ= 3.7*10⁷ Сим/м, на основе граничных условий Леонтовича-Щукина определим коэффициент затухания для заданной волны.

Формула для расчета коэффициента затухания на основе граничных условий Леонтовича-Щукина имеет вид [1]:

,

где 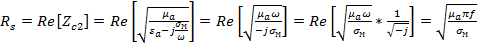- это активная часть поверхностного сопротивления волновода.

L - контур поперечного сечения металлических элементов линии передачи (рис.1). Интеграл по этому контуру разбивается на четыре интеграла. По нижней стенке при y=0, касательными будут z-я и x-я составляющие (первый и второй интегралы). По верхней стенке при x=0, касательными будут z-я и y-я составляющие (третий и четвертый интегралы).

- средний за период поток энергии через поперечное сечение трубы полученный ранее в пунке 8.

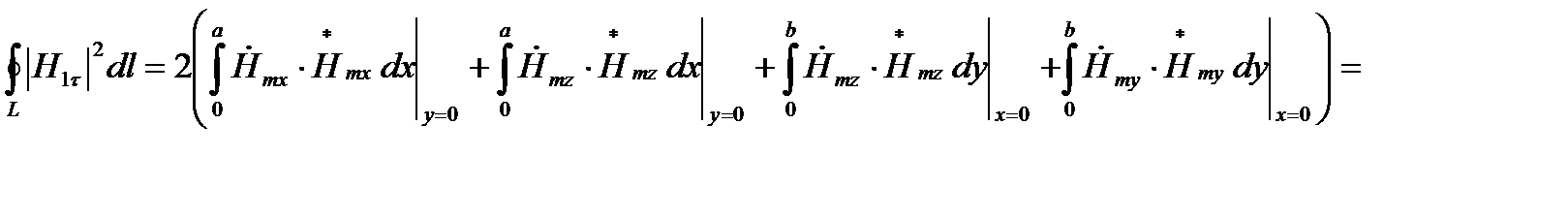
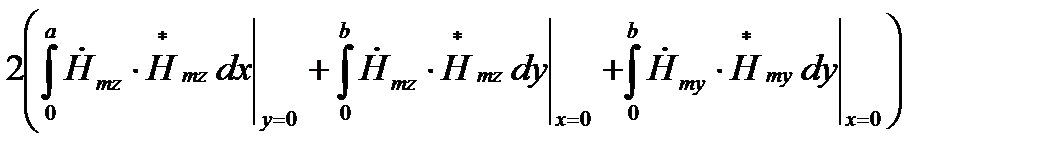
(55)

Используя соотношения (6) и (17) найдем произведение :

(56)

Используя соотношения (5) и (16) найдем произведение :

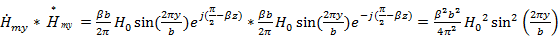(57)

Используя (56) посчитаем первый интеграл, входящий в (55):

y=0

Используя (56) посчитаем второй интеграл, входящий в (55):

x=0

Используя (57) посчитаем третий интеграл, входящий в (55):

x=0

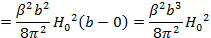
Подставляем вычисленные интегралы в выражение в (55):

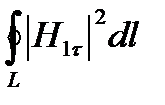
(58)

Запишем выражение для коэффициент затухания, подставив в него выражения для R_s, формулу (57) и выражение для P_Σ.cp (52).

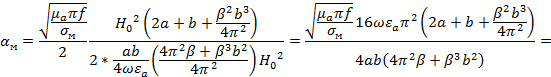
(59)

Рассчитаем коэффициент затухания, подставив в (59) численные значения входящих в выражение величин (при f=f₁):

Дата добавления: 2015-07-12