Пункт 6.

Найдем комплексные амплитуды плотностей поверхностных токов и зарядов на всех стенках трубы.

В случае идеально проводящих стенок токи проводимости являются поверхностными, а комплексная амплитуда поверхностного тока находится по формуле в соответствии с [1]:

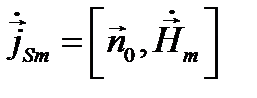
(33)

Комплексную амплитуду плотности зарядов можно найти по формуле в соответствии с [1]:

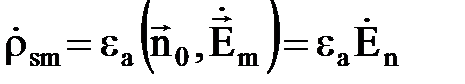(34)

1) Для нижней стенки трубы 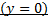(рис.1).

Нормаль совпадает с вектором : .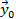

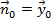Преобразуем (33):

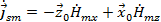(35)

Подставим в (35) полученные ранее выражения (4) и (6) с учетом того, что y=0. Тогда получим:

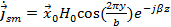
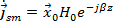(36)

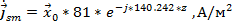
Нормальной к этой стенке составляющей вектора 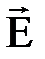будет составляющая 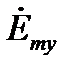. Тогда подставив в (34) выражение (11) найдем комплексную амплитуду плотности поверхностных зарядов:

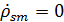(37)

2) Для верхней стенки трубы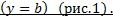

Нормаль совпадает с вектором : .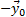

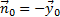Поэтому воспользуемся формулой (35) с обратным знаком и учтем, что y= b. Подставив (4) и(6) получим:

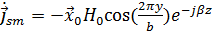
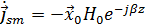(38)

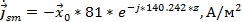
Так как нормальной составляющей вектора 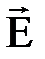будет составляющая - 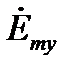(которая равна 0 из п.1) то комплексная амплитуда плотности поверхностных зарядов аналогично (37) будет равняться:

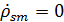(39)

3) Для правой боковой стенки (х=0) (рис.1).

Нормаль совпадает с вектором :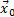

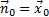
Преобразуем (33):

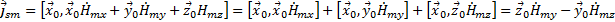
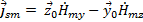(40)

Подставим в (35) полученные ранее выражения (5) и (6) с учетом того, что х=0. Тогда получим:

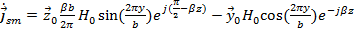(41)

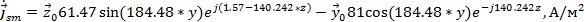
Нормальной к этой стенке составляющей вектора 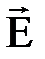будет составляющая 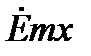, следовательно:

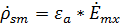(42)

Подставим в (42) формулу (10) (при x=0):

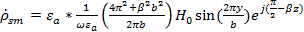
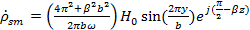(43)

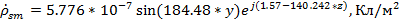
4) Для левой боковой (х=а) (рис.1).

Нормаль совпадает с вектором :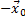

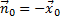
Воспользуемся формулой (40) с обратным знаком:

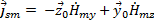(44)

Подставим в (44) выражения (5) и (6) при х=а.

(45)

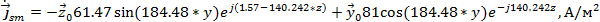
Для нахождения комплексной амплитуды плотности поверхностного заряда на этой стенке воспользуемся (42) изменив при этом знак на обратный и подставив в него (10) получим:

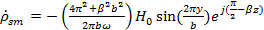(46)

Дата добавления: 2015-07-12