Пункт 1.

По условию нам задана z - составляющая вектора и входящая в нее величина .

Найдем комплексные амплитуды поперечных составляющих через соотношение, которое связывает их и данную нам величину .

Это соотношение имеет следующий вид:

Сначала найдем выражение для и подставим его в (1).

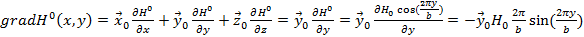(2)

Подставив (2) в (1) получим выражение для поперечных составляющих

Таким образом, мы нашли поперечные составляющие и можем записать выражения для

. Для этого нам нужно сложить поперечные составляющие (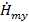) и продольную составляющую, заданную нам из условия ().

(3)

Запишем проекции комплексных амплитуд вектора на оси координат:

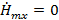(4)

(5)

(6)

Теперь нам необходимо определить комплексные амплитуды составляющих вектора . Выразим из первого уравнения Максвелла в комплексной форме:

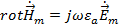тогда отсюда

(7)

Найдем

(8)

Определим выражения для частных производных, входящих в уравнение (8):

Подставим значения найденных частных производных в (8).

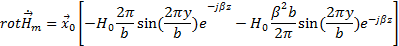
Теперь, зная выражение для 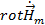мы можем найти из уравнения (7):

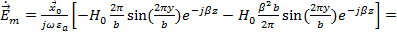
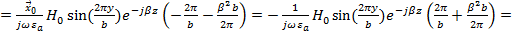
Следовательно:

(9)

Из (9) определим проекции на оси координат:

(10)

(11)

(12)

Таким образом, мы определили все составляющие комплексных амплитуд векторов и .

Дата добавления: 2015-07-12