Тема 5_2011-2012. Графический способ изображения статистических данных

Вопросы:

1. Элементы статистического графика
2. Организация числовых данных. Упорядоченный массив. Диаграмма «ствол и листья».
3. Представление числовых данных в виде таблиц и диаграмм. Гистограмма. Полигон. Полигон интегральных процентов.
4. Изображение двумерных числовых данных. Диаграмма разброса.
5. Представление категорийных данных в виде таблиц и диаграмм. Сводная таблица. Диаграмма Парето.

Вопрос 1.Элементы статистического графика

Графики в статистике – условные изображения числовых величин и их соотношений в виде различных геометрических образов – точек, линий, плоских фигур и т.п.

Основные элементы статистического графика:

1. Поле графика – место, на котором он выполняется. 1*1,3 – правило «золотого сечения»
2. Графический образ – символические знаки, с помощью которых изображаются данные
3. Пространственные и масштабные ориентиры – координатная сетка или контурные линии. Масштаб графика – это мере перевода численной величины в графическую.
4. Экспликация графика – это пояснение его содержания (название, подписи шкал).

Вопрос 2. Организация числовых данных. Упорядоченный массив. Диаграмма «ствол и листья».

Сценарий. Сравнение эффективности взаимных фондов.

В последние годы вклады во взаимные фонды (ВФ) составили миллиарды долларов. Приобретая акции (долю) взаимного фонда, инвестор вступает во владение всеми акциями компании, принадлежащими фонду. В нашем сценарии мы играем роль финансового советника, выбирающего фонд, в который следует вкладывать средства.

Цели взаимных фондов различны:

ü Капитал обычно складывается их акций схожих компаний. Например, фонды могут специализироваться на акциях крупных, средних или мелких компаний.

ü ВФ различаются по степени риска, связанного с ценными бумагами, которыми они владеют. По этому критерию фонды делятся на ВФ с очень высоким, высоким, средним, низким и очень низким уровнями риска.

Вопросы:

v Эффективность ВФ? Являются ли фонды, ориентированные на быстрый рост капитала, более эффективными, чем фонды, ориентированные на медленный рост?

v Как использовать таблицы и диаграммы для анализа эффективности различных ВФ?

Р/Е превышает среднее значение у аналогичных компаний – ориентация ВФ на быстрый рост капитала.

Здесь Р – рыночная цена в расчете на одну акцию;

Е – чистая прибыль в расчете на одну акцию.

Р/Е – характеризует скорость роста капитала.

Проанализируем данные об эффективности 259 ВФ, в т.ч. группы –

158 ВФ, ориентированных на быстрый рост капитала

101 ВФ, ориентированных на медленный рост капитала

Сравним годовые показатели доходности этих групп.

Чем больше анализируемых данных, тем труднее сконцентрировать внимание на их основных характеристиках. Для лучшего восприятия информации из набора данных, надо их правильно организовать.

Упорядоченный массив

Диаграмма «ствол и листья»

Упорядоченный массив состоит из последовательных данных, расположенных по возрастанию.

Решаемые задачи: определение мах и мин значений; типичных величин; диапазона, которому принадлежит основная масса значений.

Таблица. Упорядоченный массив из данных о пятилетней среднегодовой доходности 158 ВФ, ориентированных на быстрый рост капитала
-6,1	5,2	7,8	9,1	10,2	11,2	12,5	15,8
-2,8	5,4	7,8	9,2	10,3	11,2	12,7	16,0
-1,2	5,5	7,9	9,3	10,3	11,3	12,9	16,9
-0,7	5,8	8,1	9,3	10,4	11,3	12,9	17,0
0,5	5,9	8,1	9,5	10,5	11,3	12,9	17,0
1,8	6,0	8,2	9,5	10,5	11,3	13,0	17,6
1,9	6,2	8,3	9,5	10,5	11,4	13,1	17,8
2,5	6,3	8,3	9,5	10,5	11,5	13,2	18,1
2,8	6,5	8,4	9,6	10,5	11,5	13,4	18,1
3,3	6,5	8,5	9,6	10,5	11,5	13,4	18,2
3,5	7,0	8,5	9,7	10,6	11,6	13,7	18,5
3,8	7,1	8,5	9,8	10,7	11,7	13,7	18,5
3,8	7,1	8,6	9,9	10,7	11,7	13,9	18,7
4,0	7,2	8,8	9,9	10,8	11,9	14,1	18,9
4,2	7,2	8,8	9,9	10,9	11,9	14,7	21,4
4,3	7,3	8,8	9,9	11,0	12,2	14,8	22,0
4,5	7,5	9,0	10,0	11,0	12,2	14,9	22,9
4,6	7,6	9,0	10,1	11,1	12,3	15,0	26,3
5,0	7,6	9,1	10,1	11,1	12,3	15,7
5,1	7,8	9,1	10,1	11,1	12,4	15,8

Мин = -6,1%, мах = 26,3%. Среднегодовые показатели большинства фондов в пределах от 5 до 15%.

Диаграмма «ствол и листья» - это инструмент для организации набора данных и анализа их распределения. Данные в этой диаграмме распределены в соответствии с первыми цифрами, или стволами и замыкающими цифрами или листьями.

Например, число 10,9% состоит из ствола 10 и листа 9.

Первые два столбца – ствол, содержащий ведущие цифры чисел. Листья или замыкающие цифры, расположены справа.

Выводы по диаграмме:

1. Мин уровень пятилетней среднегодовой доходности = -6,1%
2. Ман уровень пятилетней среднегодовой доходности = 26,3%
3. Уровни доходности 158 ВФ колеблются между этими значениями, причем наибольшая концентрация доходности в интервале от 1,8 до 18,9%.
4. Количество ВФ у крайних значение невелико
5. Только 4 ВФ приносят убытки
6. Только у 4-х ВФ доходность превышает 20%

Диаграмма "ствол и листья"
Шаг:
-6
-5
-4
-3
-2
-1
-0
	8 9
	5 8
	3 5 8 8
	0 2 3 5 6
	0 1 2 4 5 8 9
	0 2 3 5 5
	0 1 1 2 2 3 5 6 6 8 8 8 9
	1 1 2 3 3 4 5 5 5 6 8 8 8
	0 0 1 1 1 2 3 3 5 5 5 5 6 6 7 8 9 9 9 9
	0 1 1 1 2 3 3 4 5 5 5 5 5 5 6 7 7 8 9
	0 0 1 1 1 2 2 3 3 3 3 4 5 5 5 6 7 7 9 9
	2 2 3 3 4 5 7 9 9 9
	0 1 2 4 4 7 7 9
	1 7 8 9
	0 7 8 8
	0 9
	0 0 6 8
	1 1 2 5 5 7 9
	0 9

Практика. Создайте диаграмму ствол и листья из приведенных ниже 7 экзаменационных оценок по маркетингу: 88 78 78 73 91 78 85

7 8 9

3888 58 1

Вопрос 3. Представление числовых данных в виде таблиц и диаграмм. Гистограмма. Полигон. Полигон интегральных процентов.

Распределим 158 ВФ, ориентированных на быстрый рост капитала, на 8 равных групп по пятилетней среднегодовой доходности

Вычислим: 1) количество ВФ в каждой группе, 2) их долю в общем количестве и 3) накопленный %, 4) серединные значения интервалов

Распределение частот для фондов быстрого роста
Карманы (верхние границы интервалов- для пятилетней среднегодовой доходности)	Число фондов	Процент, доля ВФ в общем количестве	Накопленный (Интегральный) %	Срединные точки интервалов
-5,01		0,63%	0,63%	-7,5
-0,01		1,90%	2,53%	-2,5
4,99		8,86%	11,39%	2,5
9,99		36,71%	48,10%	7,5
14,99		38,61%	86,71%	12,5
19,99		10,76%	97,47%	17,5
24,99		1,90%	99,37%	22,5
29,99		0,63%	100,00%	27,5
Итого		100%

Аналогичные расчеты выполняются для ВФ с медленным ростом капитала

Интегральные (накопленные) проценты позволяют обнаружить информацию, ускользающую от распределения частот.

Таблица. Распределение интегральных процентов для пятилетней среднегодовой доходности 101 ВФ с медленным ростом капитала и 158 ВФ с быстрым ростом капитала

Пятилетняя среднегодовая доходность	Накопленные % для ВФ с быстрым ростом капитала	Накопленные % для ВФ с медленным ростом капитала
-5	0,6
	2,5
	11,4
	48,1	36,7
	86,7	77,3
	97,5	97,1
	99,4	99,1

Выводы:

В основном пятилетняя среднегодовая доходность у ВФ с быстрым ростом капитала меньше, чем у ВФ, ориентированных на медленный рост капитала.

48,1% ВФ с быстрым ростом имеют показатели доходности не превышающие 10%. Соответствующая доля ВФ с медленным ростом капитала = 36,7%.

Гистограмма – это диаграмма, на которой изображены столбики, границы которых совпадают с границами групп.

При ее построении исследуемая случайная величина откладывается по горизонтальной оси Х, а количество элементов в соответствующих группах (их относительная частота или процентная доля), по оси вертикальной У.

Лучше один раз увидеть, чем сто раз услышать → использование графических изображений а не таблиц.

Серединные точки на гистограмме взяты из интервалов доходности.

Иногда сложно создавать диаграмму ствол и листья и гистограммы. Сложно правильно интерпретировать разницу между высотами соответствующих столбцов.

Процентный полигон – график, построенный путем соединения средних точек, соответствующих процентной доле каждой группы.

Как и при построении гистограмм, величина исследуемой переменной откладывается вдоль по горизонтальной оси, по вертикальной оси – количество элементов в каждой группе, их относительная доля или процент.

Вывод: Различия между двумя распределениями, обнаруженные ранее теперь видны четче.

Полигон накопленных (интегральных) % или кривая распределения является графическим изображением распределения суммарных процентов.

Вывод: до 20% по пятилетней доходности кривая распределения ВФ с медленным ростом капитала справа от кривой распределения доходности фондов с быстрым ростом капитала. Количество фондов с доходностью свыше 20% для этих двух групп приблизительно одинаковы.

Вопрос 4. Изображение двумерных числовых данных. Диаграмма разброса.

Диаграмма разброса – способ исследования двумерных числовых величин. Это точечная (в Excel) и корреляционная (в научной литературе) диаграмма. Полезны в разных областях деловой активности.

Пример. Специалисты по маркетингу – эффективности рекламной кампании через сравнение объемов недельных продаж и расходов на рекламу

Менеджеры по кадрам – система оплаты труда через сравнение трудового стажа сотрудников и их текущей зарплаты.

Вывод: зависимость между исследуемыми показателями положительная (или возрастающая или прямо пропорциональная).

Вопрос 5. Представление категорийных данных в виде таблиц и диаграмм. Сводная таблица. Диаграмма Парето.

При анализе категорийных или качественных данных используются способы их представления в виде таблиц и графиков.

Анализ доходности ВФ. Информация о риске, связанном с инвестированием в эти фонды.

ВФ могут иметь очень высокий, высокий, средний, низкий и очень низкий уровень риска. При работе с категорийными переменными данные вначале заносятся в сводную таблицу, а затем представляются в виде гистограмм, круговых диаграмм или диаграмм Парето.

По внешнему виду сводная таблица для категорийных данных напоминает распределение частот для числовых данных.

Виды риска для ВФ	Итого количество фондов
средний
высокий
низкий
очень высокий
очень низкий
Общий итог

Вычислим процентную долю каждой группы риска в общем итоге и накопленную (интегральную) частоту.

Риск взаимных фондов
Количество по полю Риск
Риск	Итого	Процент	Интегральный %
средний		31,66%	31,66%
высокий		30,89%	62,55%
низкий		29,34%	91,89%
очень высокий		5,79%	97,68%
очень низкий		2,32%	100,00%
Общий итог		100%

Информацию полученных таблиц можно изобразить в виде линейной диаграммы

По горизонтальной оси здесь отложено количество фондов.

Представим распределение риска инвестиций на основе имеющихся данных в виде круговой диаграммы

Цель графического представления данных – точность и ясность!

Диаграмма Парето – это особая разновидность вертикальной линейчатой диаграммы, в которой категории приводятся в порядке убывания их частот одновременно с полигоном накопленных частот. Особенно полезна, если количество исследуемых категорий велико.

Позволяет выделить наиболее важные категории из большого числа малозначимых групп.

Широкое распространение при анализе производственных процессов и контроле качества.

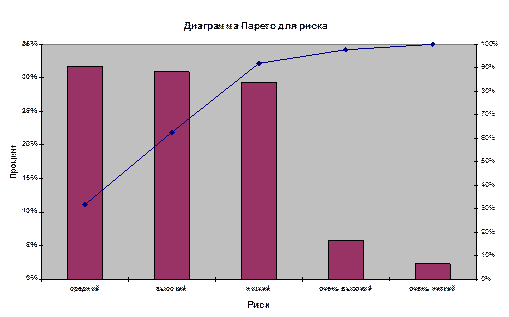
Вывод: диаграмма упорядочивает доли риска в порядке убывания. Доля фондов со средним уровнем риска = 32%. Полигон накопленных частот – 62,55% фондов имеют средний или высокий уровень риска.

Вдоль левой вертикальной оси – частоты или процентные доли. Вдоль правой вертикальной оси – накопленные частоты. По горизонтальной оси – категории. Столбцы на одинаковом расстоянии друг от друга и имеют равную ширину.

При анализе двух или двумерных категорийных переменных используют таблицы сопряженности признаков.

Представим данные в виде сводных таблиц. Здесь комиссия – плата взимаемая фондами за осуществление продаж своих акций

Сводная таблица для риска и комиссии
Количество по полю Фонд	Комиссия
Риск	Да	Нет	Общий итог
высокий
низкий
очень высокий
очень низкий
средний
Общий итог

Вывод: фонды с высоким и низким уровнями риска, как правило, взимают плату за продажу своих акций, а ВФ со средним уровнем риска как правило – нет.

Дата добавления: 2015-07-12