Методы Фурье-анализа

В основе анализа Фурье лежит разложение сигнала в частотный спектр.

В курсах математики доказывается, что любую периодическую функцию f (t) периода T можно представить в виде дискретного ряда Фурье:

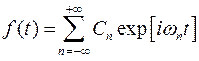, (5.5)

где круговая частота n -ой гармонической составляющей, C_n комплексная амплитуда n -ой гармоники

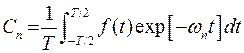. (5.6)

Совокупность коэффициентов C_n называют спектром функцииf (t); при этом | C_n | есть амплитуда гармоники частоты ω_n, arg Cn относительный фазовый сдвиг. На рис. 5.1 изображена импульсная периодическая функция f(t) и ее спектр. В общем случае, когда функция f(t) не является периодической, она может быть представлена по теореме Фурье в виде непрерывного набора гармонических колебаний с различными частотами (формула 5.7).

(5.7)

(5.8)

Рис. 5.1. Периодическая последовательность прямоугольных импульсов (а), ее спектр на интервале ¥, +¥, (b) и спектр по положительным частотам (с)

Соотношения (5.7) и (5.8) называют обратным и прямым преобразованием Фурье. В общем случае спектр F(ω) оказывается непрерывным.

Рассмотрим в качестве примера прямоугольный импульс длительности D t и амплитуды A. Спектр F(ω) (по положительным и отрицательным частотам) оказался в данном случае чисто действительным (рис. 5.2).

Рис. 5.2. Спектр одиночного прямоугольного импульса

Полуширина «главного максимума» функции F(ω) равна D ω= 2π/D t.

Пространственный двумерный спектр Фурье 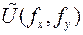является прямым преобразованием Фурье:

(5.9)

Пространственные частоты f_x и f_y имеют размерность [ м^-1 ].

По аналогии с преобразованиями Фурье для одномерного сигнала определяется обратное преобразование Фурье для двумерного оптического сигнала:

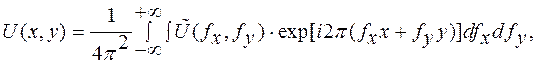(5.10)

где f_x и f_y пространственные частоты светового распределения вдоль координат x и y соответственно.

Для оцифровки сигнала обычно требуется его дискретизация (разделение) во времени.

Теорема выборки Котельникова-Шеннона гласит о том, что если непрерывный сигнал x(t) имеет спектр, ограниченный частотой F_гр, то он может быть полностью и однозначно восстановлен по его дискретным отсчетам, взятым через интервалы времени .

По аналогии с одномерным временным сигналом может быть сформулирована теорема выборки для оптического двумерного сигнала. Эта теорема доказывает, что двумерный оптический сигнал U(x,y) с ограниченной двумерной полосой пространственных частот (f_x, f_x; f_y, f_y) может быть взаимно однозначно представлен двумерным набором значений (отсчетов) , формируемых из самого сигнала, взятых через интервалы .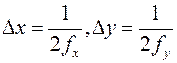

Если оптический сигнал задан в ограниченной пространственной области (X,X; Y,Y), то его спектральная функция может быть взаимно однозначно представлена двумерным набором значений, взятых через интервалы .

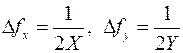Оптические преобразования Фурье изменять масштаб изображения, изменять его форму, осуществлять его сдвиг, проводить операции свертки и произведения, выполнять функция матрицы.

Для выполнения преобразований необходимо выполнять следующие требования к когерентности оптической системы:

– лазерный источник должен быть одночастотный и одномодовый,

– линзы и объективы не должны иметь фазовых неоднородностей и искажений.

Дата добавления: 2015-07-11